
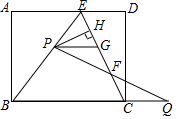
 如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.
如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.分析 (1)只要证明PG=CQ,即可根据AAS或ASA证明;
(2)结论:当x=4时,四边形PGDE是菱形.首先证明四边形PGDE是平行四边形,由PG=PE=4,即可推出四边形PGDE是菱形;
(3)①不变化.可以证明:HF=HG+FG=$\frac{1}{2}$EG+$\frac{1}{2}$CG=$\frac{1}{2}$CE=$2\sqrt{5}$;
②分两种情形讨论(Ⅰ)若△PHF∽△EAB,则$\frac{AE}{AB}=\frac{PH}{HF}$,(II)若△PHF∽△BAE,则$\frac{AB}{AE}=\frac{PH}{HF}$,分别列出方程即可解决问题;
解答 (1)证明:∵BC=BE,∴∠BCE=∠PEC,
∵PG∥BQ,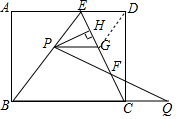
∴∠BCE=∠PGE,∠Q=∠FPG,∠QCF=∠PGF,
∴∠PGE=∠PEC,
∴PE=PG,
∵PE=CQ,
∴PG=CQ,
∴△PFG≌△QFC (ASA).
(2)结论:当x=4时,四边形PGDE是菱形.
理由如下:连结DG
∵四边形ABCD是矩形,
∴AD∥BC,
AB=CD=8,AD=BC=BE=10,
在Rt△ABE中,AE=$\sqrt{B{E^2}-A{B^2}}=\sqrt{{{10}^2}-{8^2}}=6$,
∴DE=AD-AE=10-6=4,
由(1)知PG=PE=x=4,
∴PG=DE,
∵PG∥BQ,AD∥BC,
∴PG∥DE,
∴四边形PGDE是平行四边形,
∵PG=PE=4,
∴四边形PGDE是菱形.
(3)①不变化.
理由:在Rt△ABE中,CE=$\sqrt{C{D^2}+DE{\;}^2}=\sqrt{{8^2}+{4^2}}=4\sqrt{5}$,
∵PG=PE,PH⊥EC,
∴EH=HG=$\frac{1}{2}$EG(等腰三角形“三线合一”),
∵△PFG≌△QFC,
∴CF=GF=$\frac{1}{2}$CG,
∴HF=HG+FG=$\frac{1}{2}$EG+$\frac{1}{2}$CG=$\frac{1}{2}$CE=$2\sqrt{5}$,
②∵PG∥DE,
∴∠DEC=∠PGH,
在Rt△PGH中,PH=PG×sin∠PGH=x×sin∠DEC=x×$\frac{CD}{CE}$=x×$\frac{8}{{4\sqrt{5}}}$=$\frac{{2\sqrt{5}x}}{5}$,
分两种情况讨论:
(Ⅰ)若△PHF∽△EAB,则$\frac{AE}{AB}=\frac{PH}{HF}$,
∴$\frac{6}{8}=\frac{{\frac{{2\sqrt{5}}}{5}x}}{{2\sqrt{5}}}$,
∴$x=\frac{15}{4}$,
∴当$x=\frac{15}{4}$时,△PHF∽△BAE.
(II)若△PHF∽△BAE,则$\frac{AB}{AE}=\frac{PH}{HF}$,
∴$\frac{8}{6}=\frac{{\frac{{2\sqrt{5}}}{5}x}}{{2\sqrt{5}}}$,
∴$x=\frac{20}{3}$,
∴当$x=\frac{15}{4}$或$x=\frac{20}{3}$时,△PHF与△BAE相似.
点评 本题考查相似形综合题、矩形的性质、菱形的判定和性质、全等三角形的判定和性质.相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的首先思考问题,则有不能漏解,属于中考压轴题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
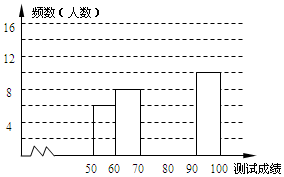 “赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 6 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 14 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com