
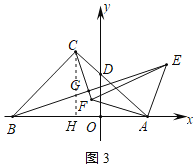
【题目】平面直角坐标系中,![]() ,
,![]() ,等腰
,等腰![]() 的顶点
的顶点![]() 在第二象限,
在第二象限,![]() 交
交![]() 轴于点
轴于点![]() .
.
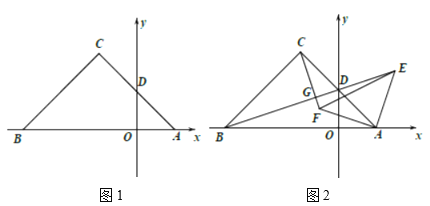
(1)如图1,求证![]() ;
;
(2)如图2,点![]() 在
在![]() 的延长线上,若点
的延长线上,若点![]() 坐标为
坐标为![]() ,以
,以![]() 为直角边在左侧作等腰
为直角边在左侧作等腰![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.
①求点![]() 的坐标;
的坐标;
②求证![]() .
.
【答案】(1)见解析;(2)①![]() ;②见解析
;②见解析
【解析】
(1)易求OA=2,OB=6,AB=8,由等腰直角三角形的性质得出∠BAC=∠ABC=45°,AC=![]() AB=
AB=![]() ,易证△AOD是等腰直角三角形,则AD=
,易证△AOD是等腰直角三角形,则AD=![]() OA=
OA=![]() ,即可得出结论;
,即可得出结论;
(2)①作EM⊥x轴于M,FN⊥x轴于N,则∠EMA=∠ANF=90°,由点E坐标为(3,3),得出OM=EM=3,由△AEF是等腰直角三角形,得出AF=AE,∠EAF=90°,证明∠FAN=∠AEM,由AAS证得△FAN≌△AEM,得出FN=AM=1,AN=EM=3,则ON=AN-OA=1,即可得出结果;
②过C作CH⊥AB于H,易求AH=CH=![]() AC=4,得C(-2,4),求出CF的解析式为:y=-3x-2,BE的解析式为:y=
AC=4,得C(-2,4),求出CF的解析式为:y=-3x-2,BE的解析式为:y=![]() x+2,得出G(
x+2,得出G(![]() ,
,![]() ),由两点间的距离公式求出GF2,EF2,EG2,根据GF2+EG2=EF2即可得出结论.
),由两点间的距离公式求出GF2,EF2,EG2,根据GF2+EG2=EF2即可得出结论.
解:(1)证明:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ;
;
(2)①作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,如图2所示,则
,如图2所示,则![]() ,
,
![]() 点
点![]() 坐标为
坐标为![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
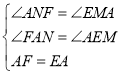 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
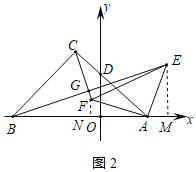
②过![]() 作
作![]() 于
于![]() ,如图3所示:
,如图3所示:
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ,
,
设直线![]() 的解析式为:
的解析式为:![]() ,
,
则![]() ,
,
解得:![]() ,
,
![]() 的解析式为:
的解析式为:![]() ,
,
设![]() 的解析式为:
的解析式为:![]() ,
,
则![]() ,
,
解得: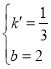 ,
,
![]() 的解析式为:
的解析式为:![]() ,
,
设![]() ,则
,则 ,
,
解得: ,
,
![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC上,点E在边AC上,且AD=AE.
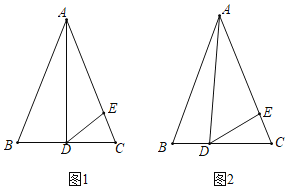
(1)如图1,当AD是边BC上的高,且∠BAD=30°时,求∠EDC的度数;
(2)如图2,当AD不是边BC上的高时,请判断∠BAD与∠EDC之间的关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意三个实数a,b,c,用min|a,b,c|表示这三个实数中最小数,例如:min|-2,0,1|=-2,则:
(1)填空,min|(-2019)0,(-![]() )-2,-
)-2,-![]() |=______,如果min|3,5-x,3x+6|=3,则x的取值范围为______;
|=______,如果min|3,5-x,3x+6|=3,则x的取值范围为______;
(2)化简:![]() ÷(x+2+
÷(x+2+![]() )并在(1)中x的取值范围内选取一个合适的整数代入求值.
)并在(1)中x的取值范围内选取一个合适的整数代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
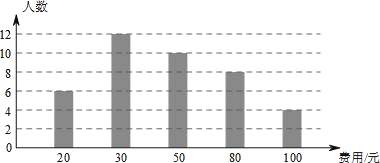
【题目】在全民读书月活动中,某校随机抽样调查了一部分学生本学期计划购买课外书的费用情况,根据图中的相关信息,解答下面问题;
(1)这次调查获取的样本容量是 ;
(2)由统计图可知,这次调查获取的样本数据的众数是 ;中位数是 ;
(3)求这次调查获取的样本数据的平均数;
(4)若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.
查看答案和解析>>
科目:初中数学 来源: 题型:
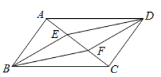
【题目】如图,在□ABCD中,E,F是对角线AC上的两点且AE=CF,在①BE=DF;②AB=DE;③BE∥DF;④四边形EBFD为菱形;⑤S△ADE=S△ABE;⑥AF=CE,这些结论中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,能够表示图中阴影部分的面积的是( )
①ac+(b﹣c)c;②ac+bc﹣c2;③ab﹣(a﹣c)(b﹣c);④(a﹣c)c+(b﹣c)c+c2

A. ①②③④ B. ①②③ C. ①② D. ①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣(2a+1)x+c(a>0)的图象经过坐标原点O,一次函数y=﹣x+4与x轴、y轴分别交于点A、B.
(1)c= ,点A的坐标为 ;
(2)若二次函数y=ax2﹣(2a+1)x+c的图象经过点A,求a的值;
(3)若二次函数y=ax2﹣(2a+1)x+c的图象与△AOB只有一个公共点,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用的练习本可在甲、乙两个商店买到.已知两个商店的标价都是每本1元,但甲商店的优惠条件是:购买10本以上,从第11本开始按标价的七折卖;乙商店的优惠条件是:从第一本开始就按标价的八五折卖.小明要买18个练习本,到__________商店买较省钱;小明现有24元,最多可买__________本练习本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到________元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com