
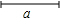 已知线段a,求作,△ABC,使AB=a,AC=BC=2a,画出图形后,测量一下∠CAB与∠CBA,猜想∠CAB与∠CBA的关系,你能说明你发现的结论吗?
已知线段a,求作,△ABC,使AB=a,AC=BC=2a,画出图形后,测量一下∠CAB与∠CBA,猜想∠CAB与∠CBA的关系,你能说明你发现的结论吗?  举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:解答题
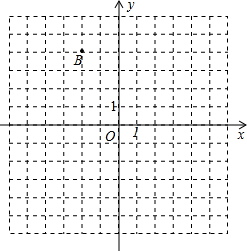 如图在直角坐标平面内,已知点A(-2,-3)与点B,将点A向右平移7个单位到达点C.
如图在直角坐标平面内,已知点A(-2,-3)与点B,将点A向右平移7个单位到达点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
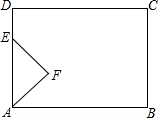 如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).
如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
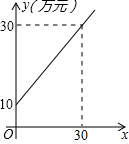 生产某种产品所需的成本y(万元)与数量x(t)之间的关系如图所示.
生产某种产品所需的成本y(万元)与数量x(t)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
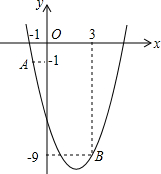 如图,已知抛物线y=ax2-4x+c的图象经过点A和点B.
如图,已知抛物线y=ax2-4x+c的图象经过点A和点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,是某市一条高逃公路上的隧道口在平面直角坐标系上的示意图,隧道的截面由抛物线和长方形构成,长方形的长是16m,宽是6m,抛物线可以用y=-$\frac{1}{32}$x2+8表示
如图所示,是某市一条高逃公路上的隧道口在平面直角坐标系上的示意图,隧道的截面由抛物线和长方形构成,长方形的长是16m,宽是6m,抛物线可以用y=-$\frac{1}{32}$x2+8表示查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com