
分析 (1)根据题意可以得到每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)根据题意可以得到P关于x的关系式,从而可以解答本题;
(3)根据题意,令利润等于6000,然后再根据P关于x的关系式,从而可以解答本题.
解答 解:(1)由题意可得,
y=700-20(x-35)=-20x+1400,
即每天的销售量y(盒)与每盒售价x(元)之间的函数关系式是y=-20x+1400;
(2)由题意可得,
P=(x-30)(-20x+1400)=-20x2+2000x-42000=-20(x-50)2+8000,
∴当x=50时,P取得最大值,此时P=8000,
即当每盒售价定为50元时,每天销售的利润P(元)最大,最大利润是8000元;
(3)由题意可得,
(x-30)(-20x+1400)=6000,
解得,x1=40,x2=60
∵P=-20(x-50)2+8000,x≤50,
∴当40≤x≤50时,销售利润不低于6000元,
∴当x=50时,销售的盒数最少,此时盒数为:-20×50+1400=400(盒),
即如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售年糕400盒.
点评 本题考查二次函数的应用,一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:填空题
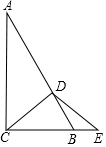 在Rt△ABC中,∠ACB=90°,∠A=30°,D为AB上一点,DC=DE交CB的延长线上于点E,若AD=7,BE=2,则∠BDE的正切值为$\frac{\sqrt{3}}{4}$.
在Rt△ABC中,∠ACB=90°,∠A=30°,D为AB上一点,DC=DE交CB的延长线上于点E,若AD=7,BE=2,则∠BDE的正切值为$\frac{\sqrt{3}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
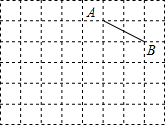 如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB,点A、B均在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
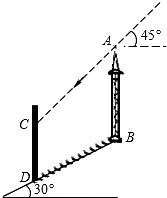 如图,在坡角为30°的山坡上有一铁塔AB,其正前方 矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为4米,落在广告牌上的影子CD的长为3米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
如图,在坡角为30°的山坡上有一铁塔AB,其正前方 矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为4米,落在广告牌上的影子CD的长为3米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com