
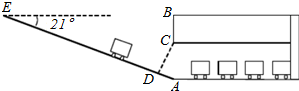
 某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为21°,斜坡AE的长为20米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.6米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).(参考数据:sin21°≈0.28,cos21°≈0.91,tan21°≈0.43)
某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为21°,斜坡AE的长为20米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.6米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).(参考数据:sin21°≈0.28,cos21°≈0.91,tan21°≈0.43) 分析 由在RT△ABE中,AE=20,∠AEB=21°,sin∠AEB=$\frac{AB}{AE}$,AB=5.6米,进而求得AC=4米,由在RT△ACD中,cos∠ACD=$\frac{CD}{AC}$,即可求得CD的长.
解答  解:在RT△ABE中,AE=20,∠AEB=21°,
解:在RT△ABE中,AE=20,∠AEB=21°,
∴∠BAE=69°,
∴sin∠AEB=$\frac{AB}{AE}$,即sin21°=$\frac{AB}{20}$,
∴AB=sin21°×20≈0.28×20=5.6,
∴AC=AB-BC=5.6-1.6=4,
在RT△ACD中,∠CAD=69°,
∴∠ACD=21°,
∴cos∠ACD=$\frac{CD}{AC}$,即cos21°=$\frac{CD}{4}$,
∴CD=cos21°×4=0.91×4≈3.6.
答:该校地下停车场的高度AC为4.0米,限高CD为3.6米.
点评 此题考查了俯角的定义.注意借助俯角构造直角三角形并解直角三角形是关键,注意数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
 如图,直线AB:y=2x+2交x轴、y轴于B、A两点,交双曲线y=$\frac{k}{x}$于C、D点,若3S△ACD=2S△ADO,求k的值.
如图,直线AB:y=2x+2交x轴、y轴于B、A两点,交双曲线y=$\frac{k}{x}$于C、D点,若3S△ACD=2S△ADO,求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
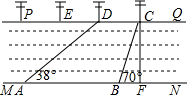 如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E…某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CF(结果精确到0.1,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).
如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E…某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CF(结果精确到0.1,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 干家务活平均时间 | 频数 | 百分比 |
| A | 10 | 25% |
| B | a | 62.5% |
| C | 5 | b |
| 合计 | c | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com