
分析 (1)根据零点值的定义即可求解;
(2)分三种情况讨论化简代数式|x+2|+|x-4|;
直接去括号,再按照去绝对值的方法去绝对值就可以了.
(3)根据(2),可得整数解;
(4)把丨x+2丨+丨x-4丨理解为:在数轴上表示x到-2和4的距离之和,求出表示-2和4的两点之间的距离即可.
解答 解:(1)∵|x+2|和|x-4|的零点值,可令x+2=0和x-4=0,解得x=-2和x=4,
∴-2,4分别为|x+2|和|x-4|的零点值.
(2)当x<-2时,|x+2|+|x-4|=-2x+2;
当-2≤x<4时,|x+2|+|x-4|=6;
当x≥4时,|x+2|+|x-4|=2x-2;
(3)∵|x+2|+|x-4|=6,
∴-2≤x≤4,
∴整数解为:-2,-1,0,1,2,3,4.
(4)|x+2|+|x-4|有最小值,
∵当x=-2时,|x+2|+|x-4|=6,
当x=4时,|x+2|+|x-4|=6,
∴|x+2|+|x-4|的最小值是6.
点评 本题主要考查了绝对值,解题的关键是能根据材料所给信息,找到合适的方法解答.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
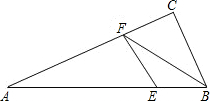 如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE:EB=4:1,EF⊥AC于F,连结FB,则tan∠CFB的值等于( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE:EB=4:1,EF⊥AC于F,连结FB,则tan∠CFB的值等于( )| A. | $\frac{5\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 5$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com