
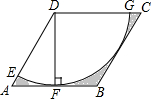
 如图,在菱形ABCD中,∠DAB=60°,AD=6,DF⊥AB,以点D为圆心,DF为半径作圆弧,分别交AD,CD于点E,G,则图中阴影部分的面积为18$\sqrt{3}$-9π(结果保留π)
如图,在菱形ABCD中,∠DAB=60°,AD=6,DF⊥AB,以点D为圆心,DF为半径作圆弧,分别交AD,CD于点E,G,则图中阴影部分的面积为18$\sqrt{3}$-9π(结果保留π)  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
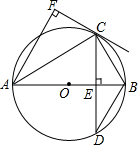 如图,AB为⊙O的直径,弦CD⊥AB,垂足为E,CF⊥AF,且CF=CE
如图,AB为⊙O的直径,弦CD⊥AB,垂足为E,CF⊥AF,且CF=CE查看答案和解析>>
科目:初中数学 来源: 题型:填空题
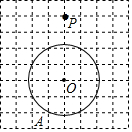 如图,网格中小正方形边长为1,点A、O、P均为格点,⊙O过点A,请过点P做⊙O的一条切线PM,切⊙O于M
如图,网格中小正方形边长为1,点A、O、P均为格点,⊙O过点A,请过点P做⊙O的一条切线PM,切⊙O于M查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-3<b-3 | B. | -a<-b | C. | -2a>-2b | D. | $\frac{1}{3}$a<$\frac{1}{3}$b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
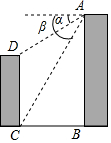 小聪家对面新建了一幢图书大厦,他在A处测得点D的俯角α为30°,测得点C的俯角β为60°(如图所示),量得两幢楼之间的水平距离BC为30米,则图书大厦CD的高度为20$\sqrt{3}$米.
小聪家对面新建了一幢图书大厦,他在A处测得点D的俯角α为30°,测得点C的俯角β为60°(如图所示),量得两幢楼之间的水平距离BC为30米,则图书大厦CD的高度为20$\sqrt{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD,AD与BC不平行,AB=CD,AC,BD为四边形ABCD的对角线,E,F,G,H分别是BD,BC,AC,AD的中点.下列结论:①EG⊥FH;②HF平分∠EHG;③EG=$\frac{1}{2}$(BC-AD);④四边形EFGH是矩形;⑤四边形EFGH是菱形.其中正确的序号是①②⑤.
如图,四边形ABCD,AD与BC不平行,AB=CD,AC,BD为四边形ABCD的对角线,E,F,G,H分别是BD,BC,AC,AD的中点.下列结论:①EG⊥FH;②HF平分∠EHG;③EG=$\frac{1}{2}$(BC-AD);④四边形EFGH是矩形;⑤四边形EFGH是菱形.其中正确的序号是①②⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
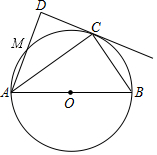 如图,⊙O的直径AB长为12,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
如图,⊙O的直径AB长为12,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com