练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】矩形的两条对角线的夹角为，对角线长为，则较短的边长为________．

    【答案】

    【解析】

    根据题意画出对应图形，∠AOD=∠BOC=60°，则∠COD=120°＞∠AOD=60°，AD是该矩形较短的一边，根据矩形的性质：矩形的对角线相等且互相平分，所以有OA=OD=OC=OB=6，又因为∠AOD=∠BOC=60°，所以AD=OA=0D=6．

    如下图所示：矩形ABCD，对角线AC=BD=12，∠AOD=∠BOC=60°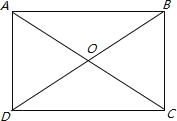

    ∵四边形ABCD是矩形
    ∴OA=OD=OC=OB=×12=6（矩形的对角线互相平分且相等）
    又∵∠AOD=∠BOC=60°，
    ∴OA=OD=AD=6，
    ∵∠COD=120°＞∠AOD=60°
    ∴AD＜DC
    所以该矩形较短的一边长为6，
    故答案是：6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰△ABC中，AB＝AC，DE垂直平分AB，分别交AB，AC于点E，D．

    （1）若∠ADE＝40°，求∠DBC的度数；

    （2）若BC＝6，△CDB的周长为15，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】列方程解应用题：

    某商场用8万元购进一批新款衬衫，上架后很快销售一空，商场又紧急购进第二批这种衬衫，数量是第一次的2倍，但进价涨了4元/件，结果共用去17.6万元．

    （1）该商场第一批购进衬衫多少件？

    （2）商场销售这种衬衫时，每件定价都是58元，剩至150件时按八折出售，全部售完．售完这两批衬衫，商场共盈利多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面图形上的任意两点，，如果经过某种变换（如：平移、旋转、轴对称等）得到新图形上的对应点，，保持，我们把这种对应点连线相等的变换称为“同步变换”．对于三种变换：

    ①平移、②旋转、③轴对称，

    其中一定是“同步变换”的有________（填序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，直线y＝x+2与x轴交于点A，与y轴交于点C．抛物线y＝ax2+bx+c的对称轴是x＝且经过A、C两点，与x轴的另一交点为点B．

    （1）求抛物线解析式．

    （2）若点P为直线AC上方的抛物线上的一点，连接PA，PC．求△PAC的面积的最大值，并求出此时点P的坐标．

    （3）抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A、M、N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场购进甲、乙两种商品，甲种商品共用了元，乙种商品共用了元．已知乙种商品每件进价比甲种商品每件进价多元，且购进的甲、乙两种商品件数相同．

    求甲、乙两种商品的每件进价；

    该商场将购进的甲、乙两种商品进行销售，甲种商品的销售单价为元，乙种商品的销售单价为元，销售过程中发现甲种商品销量不好，商场决定：甲种商品销售一定数量后，将剩余的甲种商品按原销售单价的九折销售；乙种商品销售单价保持不变．要使两种商品全部售完后共获利不少于元，问甲种商品按原销售单价至少销售多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC

    ①求证：△ABE≌△CBD；

    ②若∠CAE=30°，求∠BDC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某企业在甲地有一工厂（简称甲厂）生产某产品，2017年的年产量过万件，2018年甲厂经过技术改造，日均生产的该产品数是该厂2017年的2倍还多2件.

    （1）若甲厂2018年生产200件该产品所需的时间与2017年生产99件该产品所需的时间相同，则2017年甲厂日均生产该产品多少件？

    （2）由于该产品深受顾客欢迎，2019年该企业在乙地建立新厂（简称乙厂）生产该产品.乙厂的日均生产的该产品数是甲厂2017年的3倍还多4件.同年该企业要求甲、乙两厂分别生产m，n件产品（甲厂的日均产量与2018年相同），m:n＝14:25，若甲、乙两厂同时开始生产，谁先完成任务？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，，点是边上一点，点，是边上两点，且，作点关于的对称点点，连接，，.

    （1）依题意补全图形；

    （2）猜想______°，并证明；

    （3）猜想线段、、的数量关系______，并证明.

    查看答案和解析>>

    同步练习册答案