
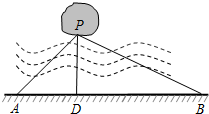
 如图,宁波市共湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请帮助小张求出小桥PD的长.($\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)
如图,宁波市共湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请帮助小张求出小桥PD的长.($\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米) 分析 设PD=x米,根据锐角三角函数的概念用x表示出AD和BD的长,根据题意列式计算即可得到答案.
解答 解:设PD=x米,
∵PD⊥AB,则∠ADP=∠BDP=90°.
在Rt△PAD中,tan∠PAD=$\frac{x}{AD}$,
故AD=$\frac{x}{tan45°}$=x,
在Rt△PBD中,tan∠PBD=$\frac{x}{DB}$,
则DB=$\frac{x}{tan30°}$=$\frac{x}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$x,
又∵AB=60米,
∴x+$\sqrt{3}$x=60,
解得:x=30$\sqrt{3}$-30≈22.0.
答:小桥PD的长度约为22.0m.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念是解题的关键,解答时,把锐角三角函数的概念理解为公式,代入公式计算即可.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题
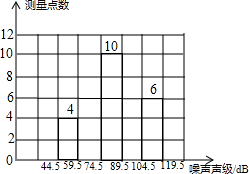 为了增强环境保护意识,在“世界环境日”当天,在环保局工作人员指导下,若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组,随机抽查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将抽查得到的数据进行整理(设所测数据是正整数),得频数分布表如表:
为了增强环境保护意识,在“世界环境日”当天,在环保局工作人员指导下,若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组,随机抽查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将抽查得到的数据进行整理(设所测数据是正整数),得频数分布表如表:| 组 别 | 噪声声级分组 | 频 数 | 频 率 |
| 1 | 44.5-59.5 | 4 | 0.1 |
| 2 | 59.5-74.5 | a | 0.2 |
| 3 | 74.5-89.5 | 10 | 0.25 |
| 4 | 89.5-104.5 | b | c |
| 5 | 104.5-119.5 | 6 | 0.15 |
| 合 计 | 40 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
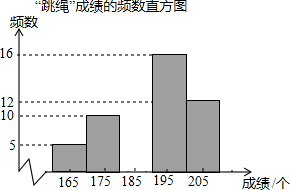 某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:
某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:| 组别 | 组中值(个) | 频数 | 频率 |
| A | 165 | 5 | 0.1 |
| B | 175 | 10 | a |
| C | 185 | b | 0.14 |
| D | 195 | 16 | c |
| E | 205 | 12 | 0.24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | C | D | |
| A | ||||
| B | ||||
| C | ||||
| D |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
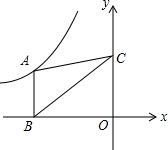 如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(k<0,x<0)的图象上,过点A作AB∥y轴交x轴于点B,点C在y轴上,连结AC、BC.若△ABC的面积是3,则k=-6.
如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(k<0,x<0)的图象上,过点A作AB∥y轴交x轴于点B,点C在y轴上,连结AC、BC.若△ABC的面积是3,则k=-6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
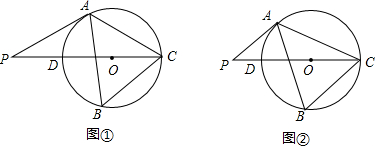
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
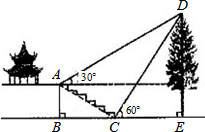 如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
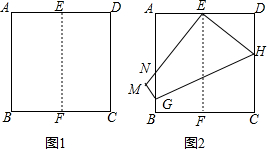 如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N.若AD=2,则MN=$\frac{1}{3}$.
如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N.若AD=2,则MN=$\frac{1}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com