
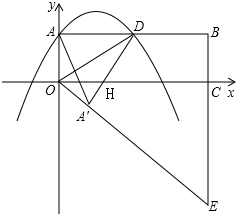
 ��ͼ����ƽ��ֱ������ϵxOy�У�����OABC�ı�OA��OC�ֱ���y���x����������ϣ��ҳ��ֱ�Ϊ1��4��DΪ��AB���е㣬һ������l������A��D����M��-1��m����
��ͼ����ƽ��ֱ������ϵxOy�У�����OABC�ı�OA��OC�ֱ���y���x����������ϣ��ҳ��ֱ�Ϊ1��4��DΪ��AB���е㣬һ������l������A��D����M��-1��m�������� ��1����ͼ1�����۵��;��εĶ�Ӧ��ƽ�У��ó���DOH=��ODH�����ԡ�OHD�ǵ��������Σ�
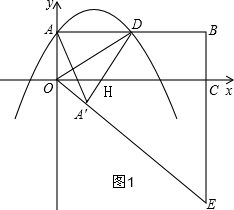
��2����ͼ2������OA��H�ĸ���A��F�����۵����A��D=2��OA��=1�����ɹ��ɶ�����A��H��A��F�ij���д����A������ꣻ
��3���ɾ��εı߳�д��A��D�����꣬���ô���ϵ�����������ߵĽ���ʽ��
��4����ͼ2������ƽ���߷��߶γɱ���������ʽ�����CE�ij�����Ϊ���������߶�CE�ཻ�����Խ���һ�����߶�CE�ϣ���ĺ�����һ��Ϊ4����x=4����ã�y=$\frac{8m-5}{3}$����-3��y��0�������в���ʽ��ó����ۣ�
���  �⣺��1����ͼ1�����۵��ã���ADO=��ODH��
�⣺��1����ͼ1�����۵��ã���ADO=��ODH��
���ı���ABCOΪ���Σ�
��AB��OC��
���ADO=��DOH��
���DOH=��ODH��
���OHD�ǵ��������Σ�
��2����ͼ2����A����A��F��x����F��
���۵��ã�A��D=AD=$\frac{1}{2}$AB=2��OA��=OA=1����OA��H=90�㣬
��A��H=x����DH=OH=2-x��
�ɹ��ɶ����ã�12+x2=��2-x��2 ��
��
x=$\frac{3}{4}$����A��H=$\frac{3}{4}$��
��DH=OH=2-$\frac{3}{4}$=$\frac{5}{4}$��
��S��A��OH=$\frac{1}{2}$OA��•A��H=$\frac{1}{2}$OH•A��F��
��1��$\frac{3}{4}$=$\frac{5}{4}$��A��F��
��A��F=$\frac{3}{5}$��
�ɹ��ɶ����ã�OF=$\sqrt{OA{��}^{2}-A��{F}^{2}}$=$\sqrt{{1}^{2}-��\frac{3}{5}��^{2}}$=$\frac{4}{5}$��
��A�䣨$\frac{4}{5}$��-$\frac{3}{5}$����
��3���������ߵĽ���ʽΪ��y=ax2+bx+c��
��A��0��1����D��2��1����M��-1��m������ã�$\left\{\begin{array}{l}{c=1}\\{4a+2b+c=1}\\{a-b+c=m}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=\frac{m-1}{3}}\\{b=\frac{2-2m}{3}}\\{c=1}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=$\frac{��m-1��{x}^{2}}{3}$+$\frac{��2-2m��x}{3}$+1��
��4����A��F��BE��
��$\frac{A��F}{CE}=\frac{OF}{OC}$��
��$\frac{\frac{3}{5}}{CE}=\frac{\frac{4}{5}}{4}$��
��CE=3��
��E��4��-3����
��x=4ʱ��y=$\frac{16��m-1��}{3}$+$\frac{4��2-2m��}{3}$+1��
y=$\frac{8m-5}{3}$��
��-3��y��0��
��-3��$\frac{8m-5}{3}$��0��
��-$\frac{1}{2}$��m��$\frac{5}{8}$��
���� �����Ƕ��κ����뼸�α任���ۺ��⣬�������۵������Ρ����������ε����ʣ��뺯�����ϣ�������Ѷȣ����õ�֪ʶ��Ҳ�϶ࣻ�����ⳣ���õ�˼·Ϊ�������۵����ϣ���δ֪�������ù��ɶ����з��̣��������εı߳����������������ijһ����ߣ��۽�ͼ���ϵĵ�������ʽ���з���������ĸϵ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ѧ������ֱ�ߺ����dz�ƽ���ߵķ���ʾ��ͼ����ͼ��ԭ����ͬλ����ȣ���ֱ��ƽ�У�
��ͼ��������ѧ������ֱ�ߺ����dz�ƽ���ߵķ���ʾ��ͼ����ͼ��ԭ����ͬλ����ȣ���ֱ��ƽ�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 Ҫ���һ����30cm����20cm��ͼ�����Ƴ�һ�����ι�ͼ����ͼ��ʾ�����������������IJ��������������Ŀ�����ȣ������Ҫʹ������ռ�����ͼ��������ķ�֮һ��Ӧ�����Ʋ����Ŀ��ȣ�������Ŀ�Ϊx cm����ôx����ķ���Ϊ��30-2x����20-2x��=30��20����1-$\frac{1}{4}$����
Ҫ���һ����30cm����20cm��ͼ�����Ƴ�һ�����ι�ͼ����ͼ��ʾ�����������������IJ��������������Ŀ�����ȣ������Ҫʹ������ռ�����ͼ��������ķ�֮һ��Ӧ�����Ʋ����Ŀ��ȣ�������Ŀ�Ϊx cm����ôx����ķ���Ϊ��30-2x����20-2x��=30��20����1-$\frac{1}{4}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
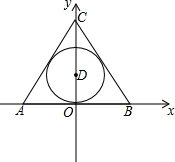 ����֪��ABC���ܳ�Ϊ42��AB=14����AB�ϵĸ�Ϊ12������������Բ�İ뾶Ϊ4
����֪��ABC���ܳ�Ϊ42��AB=14����AB�ϵĸ�Ϊ12������������Բ�İ뾶Ϊ4�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com