
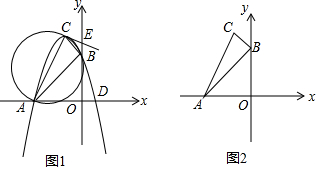
分析 (1)把B点坐标代入y=-x2-(m-1)x+m2-6得到m1=3,m2=-3,由于顶点C位于第二象限,根据对称轴得到x=-$\frac{3}{2}$<0,即m>1,所以m=3,于是得到抛物线的解析式为y=-x2-2x+3;
(2)先确定A点坐标(-3,0)和C点坐标(1,4),而B点坐标为(0,3),根据两点间的距离公式得到AB=3 $\sqrt{2}$,AC=2 $\sqrt{5}$,BC=$\sqrt{2}$,易得AB2+BC2=AC2,根据勾股定理的逆定理得∠ABC=90°,则∠CAB+∠ACB=90°,由于∠CAB=∠DCB,所以∠DCB+∠ACB=90°,于是得到CD⊥AC.
(3)存在.首先证明△BOD∽△ABC,可得当点P与点O重合时,△BPD∽△ABC;作DP′⊥BD交y轴于P′,则△BDP′∽△ABC,由直线BD的解析式为y=-3x+3,推出直线DP′的解析式为y=$\frac{1}{3}$x-$\frac{1}{3}$,可得P′(0,-$\frac{1}{3}$);作BP″⊥BD交x轴于P″,则△P″BD∽△ABC,可得直线BP″的解析式为y=$\frac{1}{3}$x+3,令y=0,得x=-9,可得P″(-9,0).由此即可解决问题.
(4)过点C作射线CF∥x轴交AB于点F,先求得直线AB的解析式,然后求得点F的坐标,当0<x<$\frac{3}{2}$时,如图1所示,依据S=S△MND-S△GNA-S△HAD可求得S与t的函数关系式,当 $\frac{3}{2}$<x≤3,如图2所示:由S=S△IVA,从而可求得S与t的函数关系式;
解答 解:(1)把B(0,3)代入y=-x2-(m-1)x+m2-6得m2-6=3,解得m1=3,m2=-3,
∵顶点C位于第二象限,
∴x=-$\frac{m-1}{2×(-1)}$<0,即m>1,
∴m=3,
∴抛物线的解析式为y=-x2-2x+3;
(2)如图1中,
令y=0,则-x2-2x+3=0,解得x1=-3,x2=1,
∴A点坐标为(-3,0),
∵y=-x2-2x+3=-(x-1)2+4,
∴C点坐标为(1,4),
而B点坐标为(0,3),
∴AB=3 $\sqrt{2}$,AC=2 $\sqrt{5}$,BC=$\sqrt{2}$,
∵(3 $\sqrt{2}$)2+( $\sqrt{2}$)2=(2 $\sqrt{5}$)2,
∴AB2+BC2=AC2,
∴∠ABC=90°,
∴AC是△ABC外接圆的直径,
∴∠CAB+∠ACB=90°,
而∠CAB=∠DCB,
∴∠DCB+∠ACB=90°,
∴CD⊥AC.
∴CD是△ABC外接圆的切线.
(3)存在.理由如下:
如图1中,∵B(0,3),D(1,0),
∴OB=3,OD=1,
∵BC=$\sqrt{2}$,AB=3$\sqrt{2}$,
∴$\frac{OD}{OB}$=$\frac{BC}{AB}$=$\frac{1}{3}$,
∴$\frac{OD}{BC}$=$\frac{OB}{AB}$,∵∠ABC=∠BOD=90°,
∴△BOD∽△ABC,
∴当点P与点O重合时,△BPD∽△ABC,
作DP′⊥BD交y轴于P′,则△BDP′∽△ABC,
∵直线BD的解析式为y=-3x+3,
∴直线DP′的解析式为y=$\frac{1}{3}$x-$\frac{1}{3}$,
∴P′(0,-$\frac{1}{3}$).
作BP″⊥BD交x轴于P″,则△P″BD∽△ABC,
∵直线BP″的解析式为y=$\frac{1}{3}$x+3,
令y=0,得x=-9,
∴P″(-9,0).
综上所述,满足条件的点P坐标为(0,0)或(0,-$\frac{1}{3}$)或(-9,0).
(4)设直线AC的解析式为y=kx+b.
∵将A(-3,0),C(-1,4)代入y=kx+b得 $\left\{\begin{array}{l}{-k+b=4}\\{-3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=6}\end{array}\right.$,
∴y=2x+6,
过点B作射线CF∥x轴交AC于点N.
∵将y=3代入直线AC的解析式得:2x+6=3,得x=-$\frac{3}{2}$,
∴F(-$\frac{3}{2}$,3).
当0<t≤$\frac{3}{2}$时,如图1所示,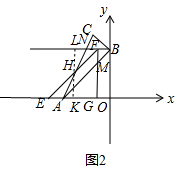
设△AOB平移到△EFG的位置,EF交AC于点H,FG交AB于点M.则OG=AE=t,过点H作LK⊥x轴于点K,交CN于点L.由△AHE∽△FHN,得
$\frac{AE}{FN}$=$\frac{HK}{HL}$,即$\frac{t}{\frac{3}{2}-t}$=$\frac{HK}{3-HK}$.
解得HK=2t
.∴S=S△EFG-S△AGM-S△AEH=$\frac{1}{2}$×3×3-$\frac{1}{2}$(3-t)2-$\frac{1}{2}$t×2t=-$\frac{3}{2}$t2+3t.
②当 $\frac{3}{2}$<t≤3时,如图2所示,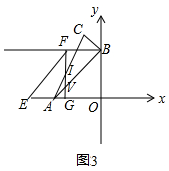
设△AOB平移到△EGF的位置,EG交AC于点I,交AB于点V.
∵直线AB的解析式为:y=x+3,直线 AC的解析式为:y=2x+6
∴V(t,t+3),I(t,-2t+6)
∴IV=-2t+6-(-t+3)=-t+3,AQ=3-t.
∴S=S△IVA=$\frac{1}{2}$IV•AG=$\frac{1}{2}$(3-t)2=$\frac{1}{2}$t2-3t+$\frac{9}{2}$,($\frac{3}{2}$<t≤3).
综上所述:S=$\left\{\begin{array}{l}{-\frac{3}{2}{t}^{2}+3t}&{(0<t≤\frac{3}{2})}\\{\frac{1}{2}{t}^{2}-3t+\frac{9}{2}}&{(\frac{3}{2}<t≤3)}\end{array}\right.$.
点评 本题考查了二次函数综合题、待定系数法、平移变换、三角形的面积、相似三角形的判定和性质、圆的有关知识,切线的判定等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的首先思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
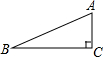 (1)如图,△ABC中,∠C=90°,那么:①∠A+∠B=90°;②tanA•tanB的值为1;
(1)如图,△ABC中,∠C=90°,那么:①∠A+∠B=90°;②tanA•tanB的值为1;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | -2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 所购苹果数量 | 不超过30千克 | 30千克以上但不超过50千克 | 50千克以上 |
| 每千克价格 | 3元 | 2.5元 | 2元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com