【答案】
分析:根据题意画出图形,如图所示,由弦AB分圆为1:5两部分,求出劣弧所对的圆心角∠AOB的度数,根据同弧所对的圆心角等于所对圆周角的2倍,求出劣弧所对的圆周角∠ACB的度数即为弦所对的一个圆周角度数;然后根据圆内接四边形的对角互补,由∠ACB的度数求出∠ADB的度数,为优弧所对的圆周角,即为弦所对的另一个圆周角,综上,得到弦所对的两个圆周角的度数.
解答: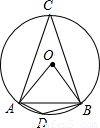
解:根据题意画出图形,如图所示:
由弦AB分圆为1:5两部分,得到
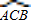
与
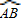
所对的圆心角度数之比为5:1,
∴劣弧所对的圆心角∠AOB=

×360°=60°,
又圆周角∠ACB和圆心角∠AOB都对
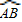
,
∴∠ACB=

∠AOB=30°;
∵四边形ADBC为圆O的圆内接四边形,
∴∠ACB+∠ADB=180°,
∴∠ADB=150°,
则弦AB所对的圆周角为30°或150°.
故答案为:30°或150°
点评:此题考查了圆周角定理,圆心角、弧及弦的关系,以及圆内接四边形的性质.对圆周角及圆心角进行相互转换是处理圆周角与圆心角问题时常用的方法,另外要求学生注意一条弦对着两条弧,对着两种圆周角.解答此类题往往借助图形,利用分类讨论的思想解决问题.

 解:根据题意画出图形,如图所示:
解:根据题意画出图形,如图所示: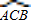 与
与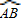 所对的圆心角度数之比为5:1,
所对的圆心角度数之比为5:1, ×360°=60°,
×360°=60°,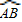 ,
, ∠AOB=30°;
∠AOB=30°;
