
【题目】把一个含45°角的直角三角板BEF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点B重合,联结DF,点M,N分别为DF,EF的中点,联结MA,MN.
(1)如图1,点E,F分别在正方形的边CB,AB上,请判断MA,MN的数量关系和位置关系,直接
写出结论;
(2)如图2,点E,F分别在正方形的边CB,AB的延长线上,其他条件不变,那么你在(1)中得到的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.


图1 图2
【答案】(1)MA=MN,MA⊥MN;(2)成立,理由详见解析
【解析】
试题(1)连接DE,先根据直角三角形的性质得出AM=![]() DF,再根据△BEF是等腰直角三角形得出AF=CE,由SAS定理得出△ADF≌△CDE,故DE=DF.再根据点M,N分别为DF,EF的中点,得出MN是△EFD的中位线,故MN=
DF,再根据△BEF是等腰直角三角形得出AF=CE,由SAS定理得出△ADF≌△CDE,故DE=DF.再根据点M,N分别为DF,EF的中点,得出MN是△EFD的中位线,故MN=![]() DE,MN∥DE,再根据平行线的性质及全等三角形的性质即可得出结论;
DE,MN∥DE,再根据平行线的性质及全等三角形的性质即可得出结论;
(2)连接DE,由直角三角形的性质得出MA=![]() DF=MD=MF,故∠1=∠3.再由点N是EF的中点,得出MN是△DEF的中位线,所以MN=
DF=MD=MF,故∠1=∠3.再由点N是EF的中点,得出MN是△DEF的中位线,所以MN=![]() DE,MN∥DE.根据△BEF是等腰直角三角形可知BF=BF,∠EBF=90°.根据SAS定理得出△ADF≌△CDE,故DF=DE,∠1=∠2,MA=MN,∠2=∠3.再根据∠2+∠4=∠ABC=90°,∠4=∠5得出∠3+∠5=90°,由三角形内角和定理可知∠6=180°﹣(∠3+∠5)=90°,故可得出结论.
DE,MN∥DE.根据△BEF是等腰直角三角形可知BF=BF,∠EBF=90°.根据SAS定理得出△ADF≌△CDE,故DF=DE,∠1=∠2,MA=MN,∠2=∠3.再根据∠2+∠4=∠ABC=90°,∠4=∠5得出∠3+∠5=90°,由三角形内角和定理可知∠6=180°﹣(∠3+∠5)=90°,故可得出结论.
试题解析:(1)解:连接DE,
∵四边形ABCD是正方形,
∴AD=CD=AB=BC,∠DAB=∠DCE=90°,
∵点M是DF的中点,
∴AM=![]() DF.
DF.
∵△BEF是等腰直角三角形,
∴AF=CE,
在△ADF与△CDE中,
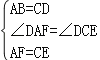 ,
,
∴△ADF≌△CDE(SAS),
∴DE=DF.
∵点M,N分别为DF,EF的中点,
∴MN是△EFD的中位线,
∴MN=![]() DE,
DE,
∴AM=MN;
∵MN是△EFD的中位线,
∴MN∥DE,
∴∠FMN=∠FDE.
∵AM=MD,
∴∠MAD=∠ADM,
∵∠AMF是△ADM的中位线,
∴∠AMF=2∠ADM.
∵△ADF≌△CDE,
∴∠ADM=∠DEC,
∴∠ADM+∠DEC+∠FDE=∠FMN+∠AMF=90°,
∴MA⊥MN.
∴MA=MN,MA⊥MN.
(2)成立.
理由:连接DE.
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°.
在Rt△ADF中,
∵点M是DF的中点,
∴MA=![]() DF=MD=MF,
DF=MD=MF,
∴∠1=∠3.
∵点N是EF的中点,
∴MN是△DEF的中位线,
∴MN=![]() DE,MN∥DE.
DE,MN∥DE.
∵△BEF是等腰直角三角形,
∴BF=BF,∠EBF=90°.
∵点E、F分别在正方形CB、AB的延长线上,
∴AB+BF=CB+BE,即AF=CE.
在△ADF与△CDE中,
∵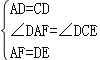
∴△ADF≌△CDE,
∴DF=DE,∠1=∠2,
∴MA=MN,∠2=∠3.
∵∠2+∠4=∠ABC=90°,∠4=∠5,
∴∠3+∠5=90°,
∴∠6=180°﹣(∠3+∠5)=90°,
∴∠7=∠6=90°,MA⊥MN.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】某家电销售商场电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商场用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13200元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,我们把横、纵坐标都为整数的点称为整点,记定点都是整点的三角形为整点三角形.如图,已知整点O(0,0),A(2,4),请在所给网格区域(含边界)上按要求画图.
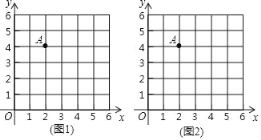
(1)在图1中画一个整点三角形OAB,其中点B在第一象限,且点B的横、纵坐标之和等于点A的横坐标;
(2)在图2中画一个整点三角形OAC,其中点C的坐标为(3t,t),且点C的横、纵坐标之和是点A的纵坐标的2倍.请直接写出△OAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF. 
(1)求证:△BOE≌△DOF;
(2)若OA= ![]() BD,则四边形ABCD是什么特殊四边形?请说明理由.
BD,则四边形ABCD是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC. 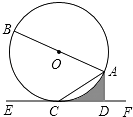
(1)求证:EF是⊙O的切线;
(2)求证:AC2=ADAB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com