
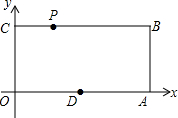
 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.分析 (1)根据三角形的面积公式即可求出△ODP的面积S;
(2)由于PB∥OD,根据平行四边形的判定可知当PB=OD=5时,四边形PODB是平行四边形,再求出PC=5,从而求出t的值;
(3)根据菱形的判定,当OD=OP=PQ=5时,ODQP为菱形,在Rt△OPC中,利用勾股定理求出CP的值,进而求出t的值及Q点的坐标;
(4)当△OPD为等腰三角形时,分三种情况进行讨论:①如果O为顶点,那么OP=OD=5;②如果P为顶点,那么PO=PD;③如果D为顶点,那么DP=DO=5.
解答 解:(1)∵O为坐标原点,A(10,0),四边形OABC为矩形,C(0,4),
∴OA=BC=10,OC=4,
∵点D是OA中点,
∴OD=DA=$\frac{1}{2}$OA=5,
∴△ODP的面积S=$\frac{1}{2}$OD•OC=$\frac{1}{2}$×5×4=10.
故答案为10;
(2)∵PB∥OD,
∴当PB=OD时,四边形PODB是平行四边形,
∵OD=5,
∴PB=5,
∴PC=BC-PB=10-5=5,
∵点P在BC上以每秒1个单位的速度由C向B运动,
∴t=5;
(3)当OD=OP=PQ=5时,ODQP为菱形,
在Rt△OPC中,由勾股定理得:
PC=$\sqrt{O{P}^{2}-O{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴t=3,CQ=CP+PQ=3+5=8,
∴Q点的坐标为(8,4);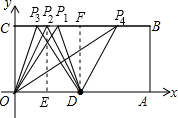 (4)△OPD为等腰三角形时,分三种情况:
(4)△OPD为等腰三角形时,分三种情况:
①如果O为顶点,那么OP=OD=5,
由勾股定理可以求得PC=3,此时P1(3,4);
②如果P为顶点,那么PO=PD,
作PE⊥OA于E,则OE=ED=2.5,此时P2(2.5,4);
③如果D为顶点,那么DP=DO=5,
作DF⊥BC于F,由勾股定理,得PF=3,
∴P3C=5-3=2或P4C=5+3=8,此时P3(2,4),P4(8,4).
综上所述,满足条件的点P的坐标为P1(3,4),P2(2.5,4),P3(2,4),P4(8,4).
点评 本题是四边形综合题,考查了矩形的性质,坐标与图形的性质,等腰三角形的性质,平行四边形的判定及性质,菱形的判定及性质,勾股定理的运用.利用数形结合、分类讨论是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 对我国初中学生视力状况的调查 | |
| B. | 对量子科学通信卫星上某种零部件的调查 | |
| C. | 对一批节能灯管使用寿命的调查 | |
| D. | 对“最强大脑”节目收视率的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25 | B. | 20 | C. | 15 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 笔试成绩 | 66 | 90 | 86 | 64 | 66 | 84 |
| 专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
| 说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com