
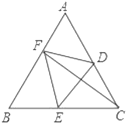
【题目】如图,在等边三角形ABC中,点D、E分别是边AC、BC上两点.将三角形ABC沿DE翻折,点C正好落在线段AB上的点F处,使得AF:BF=2:3.若BE=16,则CE的长度为( )
A.18B.19C.20D.21
【答案】B
【解析】
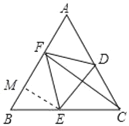
如图,作EM⊥AB于M,由等边三角形的性质可得BC=AB,∠B=60°,可得∠BEM=30°,根据含30°角的直角三角形的性质可求出BM、ME的长,根据折叠的性质可得EF=CE,设EF=CE=x,可用x表示出BC的长,根据AF:BF=2:3可用x表示出BF的长,即可表示出FM的长,在Rt△EFM中,利用勾股定理列方程求出x的值即可得答案.
如图,作EM⊥AB于M,
∵△ABC是等边三角形,
∴BC=AB,∠B=60°,
∵EM⊥AB,
∴∠BEM=30°,
∴BM=![]() BE=8,ME=
BE=8,ME=![]() BM=8
BM=8![]() ,
,
∵三角形ABC沿DE翻折,点C正好落在线段AB上的点F处,
∴FE=CE,
设FE=CE=x,
∴AB=BC=16+x,
∵AF:BF=2:3,
∴BF=![]() (16+x),
(16+x),
∴FM=BF﹣BM=![]() (16+x)﹣8=
(16+x)﹣8=![]() +
+![]() x,
x,
在Rt△EFM中,由勾股定理得:(8![]() )2+(
)2+(![]() x)2=x2,
x)2=x2,
解得:x=19,或x=﹣16(舍去),
∴CE=19.
故选B.


科目:初中数学 来源: 题型:
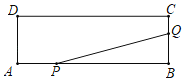
【题目】如图,矩形ABCD的两边长AB=16cm,AD=4cm,点P,Q分别从A,B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动设运动时间为x(秒),设△BPQ的面积为ycm2.
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)当△BPQ面积有最大值时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)如图①,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,BC,AC,当△BCD的面积等于△AOC面积的2倍时,求m的值;
(3)若点N为抛物线对称轴上一点,请在图②中探究抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将矩形ABCD折叠,使BC落在对角线BD上,折痕为BE,点C落在点C′处,若∠ADB=46°,则∠DBE的度数为 °.
(2)小明手中有一张矩形纸片ABCD,AB=4,AD=9.
(画一画)
如图2,点E在这张矩形纸片的边AD上,将纸片折叠,使AB落在CE所在直线上,折痕设为MN(点M,N分别在边AD,BC上),利用直尺和圆规画出折痕MN(不写作法,保留作图痕迹,并用黑色水笔把线段描清楚);
(算一算)
如图3,点F在这张矩形纸片的边BC上,将纸片折叠,使FB落在射线FD上,折痕为GF,点A,B分别落在点A′,B′处,若AG=![]() ,求B′D的长;
,求B′D的长;
(验一验)
如图4,点K在这张矩形纸片的边AD上,DK=3,将纸片折叠,使AB落在CK所在直线上,折痕为HI,点A,B分别落在点A′,B′处,小明认为B′I所在直线恰好经过点D,他的判断是否正确,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
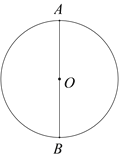
【题目】下面是小董设计的“作已知圆的内接正三角形”的尺规作图过程.
已知:⊙O.
求作:⊙O的内接正三角形.
作法:如图,
①作直径AB;
②以B为圆心,OB为半径作弧,与⊙O交于C,D两点;
③连接AC,AD,CD.
所以△ACD就是所求的三角形.
根据小董设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:在⊙O中,连接OC,OD,BC,BD,
∵OC=OB=BC,
∴△OBC为等边三角形(_______________)(填推理的依据).
∴∠BOC=60°.
∴∠AOC=180°-∠BOC=120°.
同理∠AOD=120°,
∴∠COD=∠AOC=∠AOD=120°.
∴AC=CD=AD(_______________)(填推理的依据).
∴△ACD是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
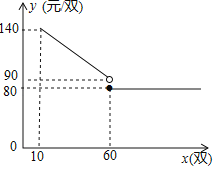
【题目】立定跳远是嘉兴市体育中考的抽考项目之一,某校九年级(1),(2)班准备集体购买某品牌的立定跳远训练鞋.现了解到某网店正好有这种品牌训练鞋的促销活动,其购买的单价y(元/双)与一次性购买的数量x(双)之间满足的函数关系如图所示.
(1)当10≤x<60时,求y关于x的函数表达式;
(2)九(1),(2)班共购买此品牌鞋子100双,由于某种原因需分两次购买,且一次购买数量多于25双且少于60双;
①若两次购买鞋子共花费9200元,求第一次的购买数量;
②如何规划两次购买的方案,使所花费用最少,最少多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西省第十五届运动会乒乓球比赛于2018年8月13日上午在山西省体育博物馆的比赛场馆内正式拉开了帷幕.第十五届运动会竞技体育组乒乓球项目产生的决赛运动员名单中太原市共27人,其中甲组有甲、乙、丙、丁四名女子运动员,若进行一次乒乓球单打比赛,要通过抽签从中选出两名运动员打第一场比赛.
(1)若已确定甲打第一场,再从其余三名运动员中随机选取一位,求恰好选中乙的概率;
(2)若两名运动员都不确定,请用树状图法或列表法,求恰好选中甲、乙两名运动员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
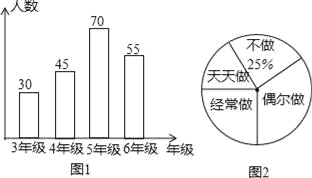
【题目】“热爱劳动,勤俭节约”是中华民族的光荣传统,某小学校为了解本校3至6年级的3000名学生帮助父母做家务的情况,以便做好引导和教育工作,随机抽取了200名学生进行调查,按年级人数和做家务程度,分别绘制了条形统计图(图1)和扇形统计图(图2).
(1)四个年级被调查人数的中位数是多少?
(2)如果把“天天做”、“经常做”、“偶尔做”都统计成帮助父母做家务,那么该校3至6年级学生帮助父母做家务的人数大约是多少?
(3)在这次调查中,六年级共有甲、乙、丙、丁四人“天天帮助父母做家务”,现准备从四人中随机抽取两人进行座谈,请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com