
【题目】如图,AD∥BC,连接BD,点E在BC上,点F在DC上,连接EF,且∠1=∠2.

(1)求证:EF∥BD;
(2)若BD平分∠ABC,∠A=130°,∠C=70°,求∠CFE的度数.
【答案】(1)证明见解析;(2)∠CFE=85°.
【解析】
(1)由AD∥BC知∠1=∠3,结合∠1=∠2得∠3=∠2,据此即可得证;
(2)由AD∥BC、∠A=130°知∠ABC=50°,再根据平分线定义及BD∥EF知∠3=∠2=25°,由三角形的内角和定理可得答案.
解:(1)如图,
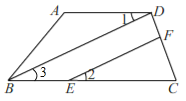
∵AD∥BC(已知),
∴∠1=∠3(两直线平行,内错角相等).
∵∠1=∠2,
∴∠3=∠2(等量代换).
∴EF∥BD(同位角相等,两直线平行).
(2)解:∵AD∥BC(已知),
∴∠ABC+∠A=180°(两直线平行,同旁内角互补).
∵∠A=130°(已知),
∴∠ABC=50°.
∵BD平分∠ABC(已知),
![]() ,
,
∴∠2=∠3=25°.
∵在△CFE中,∠CFE+∠2+∠C=180°(三角形内角和定理),∠C=70°,
∴∠CFE=85°.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一种广场三联漫步机,其侧面示意图如图2所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°.求点D到地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件不能判定四边形ABCD是矩形的是( )

A.∠DAB=∠ABC=∠BCD=90°B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DOD.AO=BO=CO=DO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD在平面直角坐标系中,点A(1,8),B(1,6),C(7,6).
(1)请直接写出D点的坐标.
(2)连接OB,OD,BD,请求出三角形OBD的面积.
(3)若长方形ABCD以每秒1个单位长度的速度向下运动,当边BC与x轴重合时,停止运动,设运动的时间为t秒,t为多少时,三角形OBD的面积等于长方形ABCD的面积的![]() ?
?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
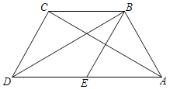
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,AB=2,求菱形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小正方形的边长都是1,三角形ABC三个顶点与方格纸中小正方形的顶点重合,请在方格纸中分别画出符合要求的图形,具体要求如下:
(1)在图①中平移三角形ABC,点A移动到点P,画出平移后的三角形PMN;
(2)在图②中将三角形ABC三个顶点的横、纵坐标都减去2,画出得到的三角形A1B1C1;
(3)在图③中建立适当的平面直角坐标系,且A点的坐标为(0,2),C点的坐标为(1,5).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现计划把1240吨甲种货物和880吨乙种货物用一列火车运往某地,已知这列火车挂有A、B两种不同规格的货车车厢共40节,使用A型车厢每节费用为6000元,B型车厢每节费用8000元.如果每节A型车厢最多可装35吨甲种货物和15吨乙种货物,每节B型车厢最多可装25吨甲种货物和35吨乙种货物;
(1)那么共有哪几种安排车厢的方案?
(2)在上述方案中,哪种方案运费最省、最少运费为多少元?
(3)在(1)问下,若两种货物全部售出,且每吨货物售出获利200元,除去运费获
利154000元,问:在这种情况下是按哪种方案安排车厢的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com