
| A. | $\left\{{\begin{array}{l}{x=4}\\{y=6}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=5}\\{y=6}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=5}\\{y=10}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=10}\\{y=15}\end{array}}\right.$ |
分析 先根据方程组$\left\{{\begin{array}{l}{{a_1}x+{b_1}y={c_1}}\\{{a_2}x+{b_2}y={c_2}}\end{array}}\right.$的解为$\left\{{\begin{array}{l}{x=4}\\{y=6}\end{array}}\right.$,得到$\left\{\begin{array}{l}{20{a}_{1}+30{b}_{1}=5{c}_{1}}\\{20{a}_{2}+30{b}_{2}=5{c}_{2}}\end{array}\right.$,进而得到$\left\{\begin{array}{l}{20=4x}\\{30=3y}\end{array}\right.$,求得$\left\{\begin{array}{l}{x=5}\\{y=10}\end{array}\right.$.
解答 解:∵方程组$\left\{{\begin{array}{l}{{a_1}x+{b_1}y={c_1}}\\{{a_2}x+{b_2}y={c_2}}\end{array}}\right.$的解为$\left\{{\begin{array}{l}{x=4}\\{y=6}\end{array}}\right.$,
∴$\left\{\begin{array}{l}{4{a}_{1}+6{b}_{1}={c}_{1}}\\{4{a}_{2}+6{b}_{2}={c}_{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{20{a}_{1}+30{b}_{1}=5{c}_{1}}\\{20{a}_{2}+30{b}_{2}=5{c}_{2}}\end{array}\right.$,
又∵方程组$\left\{{\begin{array}{l}{4{a_1}x+3{b_1}y=5{c_1}}\\{4{a_2}x+3{b_2}y=5{c_2}}\end{array}}\right.$,
∴$\left\{\begin{array}{l}{20=4x}\\{30=3y}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=5}\\{y=10}\end{array}\right.$,
故选:C.
点评 本题主要考查了二元一次方程组的解,解题时注意:当遇到有关二元一次方程组的解的问题时,通常采用代入法,即将解代入原方程组,这种方法主要用在求方程中的字母系数.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
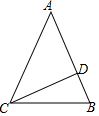 从等腰三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的黄金分割线.
从等腰三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的黄金分割线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
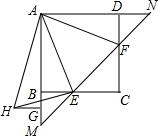 如图,在矩形ABCD中,点E、F分别在边BC、CD上,且EF分别与AB、AD的延长线交于点M、N,∠EAF=∠CEF=45°.点G在边AB的延长线上,将△ADF绕着点A按顺时针方向旋转90°后能与△AGH重合,连接EH.
如图,在矩形ABCD中,点E、F分别在边BC、CD上,且EF分别与AB、AD的延长线交于点M、N,∠EAF=∠CEF=45°.点G在边AB的延长线上,将△ADF绕着点A按顺时针方向旋转90°后能与△AGH重合,连接EH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com