
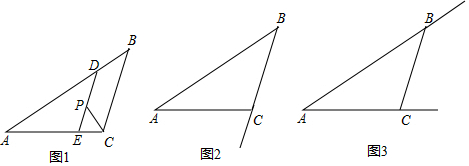
分析 (1)利用CP是∠ACB的平分线,得出∠ACP=∠BCP,又由于DE∥BC,得出∠CPE=∠FCP,即∠ACP=∠CPE,进而得出EP=EC,同理得出DP=DB,即可得出结论;
(2)同(1)的方法即可得出结论;
(3)同(1)(2)的方法即可得出结论.
解答 解(1)结论:DE=CE+BD;理由如下:
如图1, ∵CP是∠ACB的平分线,
∵CP是∠ACB的平分线,
∴∠ACP=∠BCP,
∵DE∥BC,
∴∠CPE=∠BCP,
∴∠ACP=∠CPE,
∴EP=EC,
∵BP是∠ABC的平分线,
∴∠ABP=∠CBP,
∵DE∥BC,
∴∠DPB=∠CBP,
∴∠ABP=∠DPB,
∴DP=DB,
∴DE=EP+DP=EC+DB,
即:DE=CE+BD;
(2)补全图形如图2,
结论:DE=BD-CE,理由如下:
∵CP是∠ACB的外角∠ACF的平分线,
∴∠ACP=∠FCP,
∵DE∥BC,
∴∠CPE=∠FCP,
∴∠ACP=∠CPE,
∴EP=EC,
∵BP是∠ABC的平分线,
∴∠ABP=∠CBP,
∵DE∥BC,
∴∠DPB=∠CBP,
∴∠ABP=∠DPB,
∴DP=DB,
∴DE=DP-PE=DB-CE
即:DE=BD-CE;
(3) 补全图形如图3,
补全图形如图3,
结论:DE=BD+CE,理由如下:
∵CP是∠ACB的外角∠BCE的平分线,
∴∠BCP=∠ECP,
∵DE∥BC,
∴∠CPE=∠BCP,
∴∠ECP=∠CPE,
∴EP=EC,
∵BP是∠ABC的外角∠CBD的平分线,
∴∠DBP=∠CBP,
∵DE∥BC,
∴∠DPB=∠CBP,
∴∠DBP=∠DPB,
∴DP=DB,
∴DE=DP+PE=DB+CE.
故答案为:DE=BD+CE.
点评 此题是三角形综合题,主要考查了角的平分线,平行线的性质,等腰三角形的判定;判断出DP=BD和EP=CE是解本题关键.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题
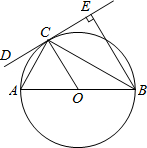 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,BE⊥CD,垂足为E,连接AC、BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,在正方形ABCD中,E、F分别为DC、BC边上的点,且满足∠EAF=45°,连结EF.
如图1,在正方形ABCD中,E、F分别为DC、BC边上的点,且满足∠EAF=45°,连结EF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
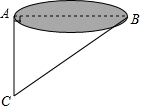 如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.
如图,某学校数学课外活动小组的同学们,为了测量一个小湖泊两岸的两棵树A和B之间的距离,在垂直AB的方向AC上确定点C,如果测得AC=75米,∠ACB=55°,那么A和B之间的距离是( )米.| A. | 75•sin55° | B. | 75•cos55° | C. | 75•tan55° | D. | $\frac{75}{tan55°}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com