
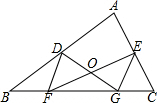
 如图,在△ABC中D,E分别是AB,AC的中点,点F,G在BC上,且BC=4BF=4CG,EF与DG相交于点O,若∠DFE=40°,∠DGE=80°,那么∠DOE的度数是( )
如图,在△ABC中D,E分别是AB,AC的中点,点F,G在BC上,且BC=4BF=4CG,EF与DG相交于点O,若∠DFE=40°,∠DGE=80°,那么∠DOE的度数是( )| A. | 100° | B. | 120° | C. | 140° | D. | 160° |
分析 连接DE,利用中位线的性质,可得DE=$\frac{1}{2}BC$,由BC=4BF=4CG可得FG=$\frac{1}{2}BC$,易得DE∥FG且DE=FG,易得四边形DEFG为平行四边形,可得DF∥EG,利用平行线的性质可得∠DGE=∠FDG,由外角的性质可得结果.
解答 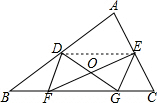 解:连接DE,
解:连接DE,
∵D,E分别是AB,AC的中点,
∴DE∥BC且DE=$\frac{1}{2}BC$,
∵BC=4BF=4CG,
∴FG=$\frac{1}{2}BC$,
∴四边形DEFG为平行四边形,
∴DF∥EG,
∴∠DGE=∠FDG=80°,
∵∠DFE=40°,
∴∠DOE=80°+40°=120°,
故选B.
点评 本题主要考查了中位线的性质,得出四边形DEFG为平行四边形是解答此题的关键.


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
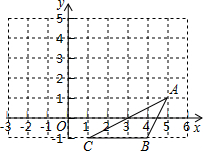 已知,△ABC在直角坐标系中的位置如图所示,现将△ABC先向上平移3个单位,再向左平移2个单位.
已知,△ABC在直角坐标系中的位置如图所示,现将△ABC先向上平移3个单位,再向左平移2个单位.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某超市为了测定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为7.
某超市为了测定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成如下的频数分布直方图(图中等待时间2分钟到3分钟表示大于或等于2分钟而小于3分钟,其它类同).这个时间段内顾客等待时间不少于6分钟的人数为7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲种 | B. | 乙种 | C. | 丙种 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com