
【题目】如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC. 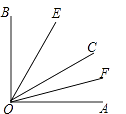
(1)若∠AOB=90°,∠AOC=40°,求∠EOF的度数;
(2)若∠AOB=a,求∠EOF的度数.
【答案】
(1)解:∠BOC=∠AOB﹣∠AOC=90°﹣40°=50°,
∵OE平分∠BOC,OF平分∠AOC,
∴∠EOC= ![]() ∠BOC=
∠BOC= ![]() ×50°=25°,∠COF=
×50°=25°,∠COF= ![]() ∠AOC=
∠AOC= ![]() ×40°=20°,
×40°=20°,
∴∠EOF=∠EOC+∠COF=25°+20°=45°
(2)解:∵OE平分∠BOC,OF平分∠AOC,
∴∠EOC= ![]() ∠BOC,∠COF=
∠BOC,∠COF= ![]() ∠AOC,
∠AOC,
∴∠EOF=∠EOC+∠COF= ![]() ∠BOC+
∠BOC+ ![]() ∠COF=
∠COF= ![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)= ![]() ∠AOB=
∠AOB= ![]() α
α
【解析】(1)首先求得∠BOC,然后根据角的平分线的定义求得∠EOC和∠COF,然后根据∠EOF=∠EOC+∠COF求解;(2)根据角的平分线的定义求得∠EOC= ![]() ∠BOC,∠COF=
∠BOC,∠COF= ![]() ∠AOC,然后根据∠EOF=∠EOC+∠COF=
∠AOC,然后根据∠EOF=∠EOC+∠COF= ![]() ∠BOC+
∠BOC+ ![]() ∠COF=
∠COF= ![]() (∠BOC+∠AOC)即可求解.
(∠BOC+∠AOC)即可求解.
【考点精析】关于本题考查的角的平分线,需要了解从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(m-2)x2-4x-2=0有两个实数根,则实数m的取值范围是( )
A. m≥0B. m>0C. m≥0,m≠2D. m>0,m≠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E、F分别在BC、AD上,且∠BAE=∠DCF.
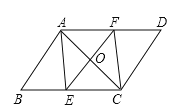
(1)求证:△ABE≌△CDF;
(2)若AC⊥EF,试判断四边形AECF是什么特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年南京青奥会某项目6名礼仪小姐的身高如下(单位:cm):168,166,168,167,169,168,则她们身高的众数是cm,极差是cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com