
【题目】概念学习
规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
理解概念
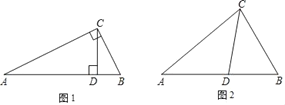
(1)如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,请写出图中两对“等角三角形”.
概念应用
(2)如图2,在△ABC中,CD为角平分线,∠A=40°,∠B=60°.求证:CD为△ABC的等角分割线.
(3)在△ABC中,∠A=42°,CD是△ABC的等角分割线,直接写出∠ACB的度数.
【答案】(1)△ABC与△ACD,△ABC与△BCD,△ACD与△BCD是“等角三角形”;(2)见解析;(3)∠ACB的度数为111°或84°或106°或92°
【解析】
(1)根据题中给出的“等角三角形”的定义即可解答;
(2)通过三角形内角和定理求出∠ACB为80°,然后再由角平分线的定义可得到∠ACD=∠DCB=![]() ∠ACB=40°,最后通过 “等角分割线”的定义进行证明;
∠ACB=40°,最后通过 “等角分割线”的定义进行证明;
(3)需分情况讨论,当△ACD是等腰三角形时DA=DC或DA=AC,当△BCD是等腰三角形时DB=BC或DC=BD,然后根据等腰三角形的性质和三角形的内角和定理进行求解.
解:(1)△ABC与△ACD,△ABC与△BCD,△ACD与△BCD是“等角三角形”;
(2)∵在△ABC中,∠A=40°,∠B=60°
∴∠ACB=180°﹣∠A﹣∠B=80°
∵CD为角平分线,
∴∠ACD=∠DCB=![]() ∠ACB=40°,
∠ACB=40°,
∴∠ACD=∠A,∠DCB=∠A,
∴CD=DA,
∵在△DBC中,∠DCB=40°,∠B=60°,
∴∠BDC=180°﹣∠DCB﹣∠B=80°,
∴∠BDC=∠ACB,
∵CD=DA,∠BDC=∠ACB,∠DCB=∠A,
∠B=∠B,
∴CD为△ABC的等角分割线;
(3)当△ACD是等腰三角形,DA=DC时,∠ACD=∠A=42°,
∴∠ACB=∠BDC=42°+42°=84°,
当△ACD是等腰三角形,DA=AC时,∠ACD=∠ADC=69°,
∠BCD=∠A=42°,
∴∠ACB=69°+42°=111°,
当△BCD是等腰三角形,DC=BD时,∠ACD=∠BCD=∠B=46°,
∴∠ACB=92°,
当△BCD是等腰三角形,DB=BC时,∠BDC=∠BCD,
设∠BDC=∠BCD=x,
则∠B=180°﹣2x,
则∠ACD=∠B=180°﹣2x,
由题意得,180°﹣2x+42°=x,
解得,x=74°,
∴∠ACD=180°﹣2x=32°,
∴∠ACB=106°,
∴∠ACB的度数为111°或84°或106°或92°.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
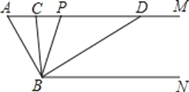
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级开展“社会主义核心价值观”演讲比赛活动,九(1)班、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出5名选手的复赛成绩(满分100分)如图所示.

根据图中数据解决下列问题:
(1)九(1)班复赛成绩的众数是 分,九(2)班复赛成绩的中位数是 分;
(2)请你求出九(1)班和九(2)班复赛的平均成绩和方差,并说明哪个班的成绩更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
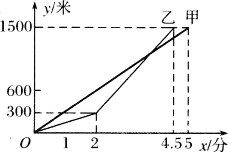
【题目】甲、乙两人进行1500米比赛,在比赛时,两人所跑的路程y(米)与所用的时间x(分)间的函数关系如图所示,解答下列问题:
(1)求甲的速度等于多少米/分;
(2)当乙到终点时,甲距离终点有多远;
(3)乙在距终点多远处追上了甲.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(﹣2)﹣1﹣|﹣![]() |+(
|+(![]() ﹣1)0+cos45°.
﹣1)0+cos45°.
(2)已知m2﹣5m﹣14=0,求(m﹣1)(2m﹣1)﹣(m+1)2+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点在数轴上,点A在原点O的左边,表示的数为﹣10,点B在原点的右边,且BO=3AO.点M以每秒3个单位长度的速度从点A出发向右运动.点N以每秒2个单位长度的速度从点O出发向右运动(点M,点N同时出发).
(1)数轴上点B对应的数是 ,点B到点A的距离是 ;
(2)经过几秒,原点O是线段MN的中点?
(3)经过几秒,点M,N分别到点B的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
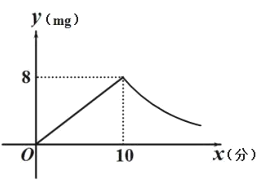
【题目】为预防传染病,某校定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量 ![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 成正比例;燃烧后,
成正比例;燃烧后,![]() 与
与![]() 成反比例(如图所示).现测得药物
成反比例(如图所示).现测得药物![]() 分钟燃完,此时教室内每立方米空气含药量为
分钟燃完,此时教室内每立方米空气含药量为![]() .根据以上信息解答下列问题:
.根据以上信息解答下列问题:
(1)分别求出药物燃烧时及燃烧后 ![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)当每立方米空气中的含药量低于![]() 时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
(3)当室内空气中的含药量每立方米不低于![]() 的持续时间超过
的持续时间超过![]() 分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com