
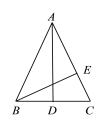
【题目】在三角形ABC中,AB=AC,D是底边上的中点,BE垂直AC于点E,①∠ABC=∠ACB;②AD⊥BC;③∠BAD=∠CBE;④AB=2BD,其中正确的有___________.
【答案】①②③
【解析】
如图所示,由AB=AC,根据“等边对等角”得到①结论正确;由AB=AC,D为BC中点,根据等腰三角形“三线合一”的性质得到AD⊥BC,得到②结论正确;在△ABD和△BCE中根据已知条件和三角形内角和定理可以得到③结论正确;AB和BD无数量关系,得到④结论错误.
①∵AB=AC,
∴∠ABC=∠ACB,①结论正确;
②∵AB=AC,D为BC中点,
∴AD⊥BC,②结论正确;
③∵AB=AC,
∴∠ABC=∠ACB,
∵AB=AC,D为BC中点,
∴AD⊥BC,
∵BE⊥AC,
∴∠ADB=∠BEC,
∴∠BAD=∠CBE,③结论正确;
④AB与BD无数量关系,故④错误.
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】某书店响应国家“中华优秀传统文化经典进书店”的号召,用2100元购进某经典读本若干套,很快售完,该店又用4500元购进第二批该经典读本若干套,进货量是第一批的2倍,但每套的进价比第一批提高了10元.求:
(1)该店这两批经典读本各购进多少套?
(2)若第一批该经典读本的售价是170元套,该店经理想让这两批经典读本售完后的总利润不低于1950元,则第二批该经典读本每套至少要售多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.
(1)求证:AD平分∠BAC;
(2)连接EF,求证:AD垂直平分EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,对称轴为直线x= ![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时: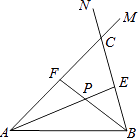
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32 ![]() ,求AQ的长.
,求AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数 ![]() 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( ) 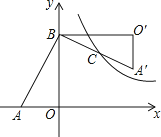
A.3
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬荆州优秀传统文化,某中学举办了荆州文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答为得分、不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
组别 | 分数段 | 频数(人) | 频率 |
1 | 50≤x<60 | 30 | 0.1 |
2 | 60≤x<70 | 45 | 0.15 |
3 | 70≤x<80 | 60 | n |
4 | 80≤x<90 | m | 0.4 |
5 | 90≤x<100 | 45 | 0.15 |
请根据以图表信息,解答下列问题: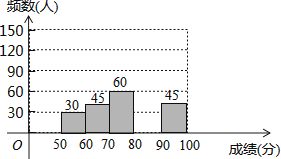
(1)表中m= , n=;
(2)补全频数分布直方图;
(3)全体参赛选手成绩的中位数落在第几组;
(4)若得分在80分以上(含80分)的选手可获奖,记者从所有参赛选手中随机采访1人,求这名选手恰好是获奖者的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图①是边长为1的等边三角形纸板,周长记为C1,沿图①的底边剪去一块边长为![]() 的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形,得到图②,周长记为C2,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的![]() ),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.
),得图③④…,图n的周长记为Cn,若n≥3,则Cn-Cn-1=_____.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明一家利用国庆八天驾车到某景点旅游,小汽车出发前油箱有油35L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图像回答下列问题:
(1)小汽车行驶______h后加油,中途加油_______L
(2)求加油前油箱余油量Q与行驶时间t的函数关系式
(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速80km/h,要到达目的地,油箱中的油是否够用?请说明理由

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com