
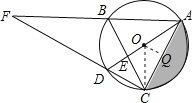
【题目】(本题满分10分)如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°,请解答下列问题:

(1)求∠CAD的度数;
(2)设AD、BC相交于E,AB、CD的延长线相交于F,求∠AEC、∠AFC的度数;
(3)若AD=6,求图中阴影部分的面积.
【答案】(1)30°;(2)∠AEC=100°,∠AFC=20°;(3)![]() .
.
【解析】试题分析:
(1)根据圆周角定理求出∠ADC、∠ACD的度数,相减即可;
(2)根据三角形的内角和定理求出∠BAC,根据三角形的外角性质求出即可;
(3)连接OC,过O作OQ⊥AC于Q,求出∠AOC的度数,求出高OQ和弦AC,求出扇形和三角形的面积,相减即可.
试题解析:
:(1)∵弧AC=弧AC,
∴∠ADC=∠ABC=60°,
∵AD是直径,
∴∠ACD=90°,
∴∠CAD=180°-∠ACD-∠ADC=30°,
答:∠CAD的度数是30°.
(2)∵∠BAC=180°-∠ABC-∠ACB=70°,
∴∠BAD=∠BAC-∠CAD=70°-30°=40°,
∴∠BCD=∠BAD=40°,
∴∠AEC=∠ADC+∠BCD=100°,
∵∠AFC=∠ABC-∠BCF=60°-40°=20°,
答:∠AEC=100°,∠AFC=20°.
连接OC,过O作OQ⊥AC于Q,
∵∠CAD=30°,AO=3,
∴OQ=![]()
由勾股定理得:AQ=![]()
由垂径定理得:AC=2AQ=![]()
∵∠AOC=2∠ABC=120°,
∴阴影部分的面积是S扇形OAC-S△AOC=![]() .
.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】(本题满分6分)
小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4和黑桃的1,2,3,4。小明建议:“我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为偶数我得1分,先得到10分的获胜”。这个游戏对小亮和小明公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级上学期期末考试数学成绩,从九年级学生中随机抽取了部分学生进行调查,并将所抽取的学生数学成绩(成绩均为整数)分为A、B、C、D、E五个等级,A:50.5~60.5,B:60.5~70.5,C:70.5~80.5,D:80.5~90.5,E:90.5~100.5,并绘制了如图所示的频数分布直方图和扇形统计图,请你根据统计图提供的信息解答下列问题: 
(1)这次抽样调查共抽取了多少名学生?
(2)请把频数分布直方图补充完整;
(3)这次期末考试数学成绩的中位数落在哪个等级内?
(4)该校九年级有800名学生,若规定80分以上(不含80分)为良好,试估计九年级有多少名学生的数学成绩为良好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+x+2经过点(-1,0).
(1)求a的值,并写出这条抛物线的顶点坐标.
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com