
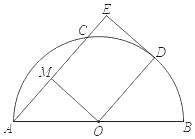
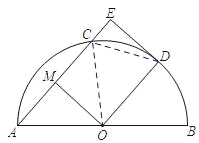
【题目】如图,AB是半⊙O的直径,点C,D为半圆O上的点,AE||OD,过点D的⊙O的切线交AC的延长线于点E,M为弦AC中点
(1)填空:四边形ODEM的形状是 ;
(2)①若![]() ,则当k为多少时,四边形AODC为菱形,请说明理由;
,则当k为多少时,四边形AODC为菱形,请说明理由;
②当四边形AODC为菱形时,若四边形ODEM的面积为4![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)四边形AODC为菱形,见解析;(2)①当k为1时,四边形AODC为菱形.理由见解析;②⊙O的半径为2![]() .
.
【解析】
(1)运用切线定理、垂径定理、平行线的性质证明四个角均为90°,即可说明四边形ODEM为矩形;
(2)①当k为1时,四边形AODC为菱形.连接CD,CO.由四边形AODC为菱形,可得AO=OD=CD=AC,由OM垂直平分AC,得到OA=OC,所以OA=OC=AC,因此△OAC为等边三角形,于是∠CAO=60°,∠CDO=60°,∠ECD=30°,
所以CE=![]() CD=
CD=![]() AC,又CM=
AC,又CM=![]() AC,因此CE=CM,即
AC,因此CE=CM,即
![]() =1,所以当k为1时,四边形AODC为菱形;
=1,所以当k为1时,四边形AODC为菱形;
②由四边形ODEM的面积为4![]() ,可知ODMO=43,由①四边形AODC为菱形时,∠MAO=60°,所以
,可知ODMO=43,由①四边形AODC为菱形时,∠MAO=60°,所以![]() =sin∠MAO=sin60°,MO=AOsin60°=
=sin∠MAO=sin60°,MO=AOsin60°=![]() AO,因此ODMO=OA
AO,因此ODMO=OA
![]() OA=4
OA=4![]() ,所以OA=2
,所以OA=2![]() .
.
(1)∵DE是⊙O的切线,
∴OD⊥DE,∠ODE=90°,
∵M为弦AC中点,
∴OM⊥AC,∠OME=90°,
∵AE||OD,
∴∠E=90°,∠MOD=90°,
∴四边形ODEM是矩形;
(2)①当k为1时,四边形AODC为菱形.
理由如下:
连接CD,CO.
∵四边形AODC为菱形,
∴AO=OD=CD=AC,
∵OM垂直平分AC,
∴OA=OC,
∴OA=OC=AC,
∴△OAC为等边三角形,
∴∠CAO=60°,∠CDO=60°,
∴∠ECD=30°,
∴CE=![]() CD=
CD=![]() AC,
AC,
∵CM=![]() AC,
AC,
∴CE=CM,
∴![]() ,
,
当k为1时,四边形AODC为菱形;
②∵四边形ODEM的面积为![]() ,
,
∴ODMO=![]() ,
,
由①四边形AODC为菱形时,∠MAO=60°,
∴![]() ,MO=AOsin60°=
,MO=AOsin60°=![]() AO,
AO,
∴ODMO=![]() ,
,
∴OA=2![]() ,
,
∴⊙O的半径为2![]() .
.


科目:初中数学 来源: 题型:
【题目】某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:
月份(x) | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
销售量(p) | 3.9万台 | 4.0万台 | 4.1万台 | 4.2万台 | 4.3万台 | 4.4万台 |
(1)求p关于x的函数关系式;
(2)求该品牌手机在去年哪个月的销售金额最大?最大是多少万元?
(3)今年1月份该品牌手机的售价比去年12月份下降了m%,而销售量也比去年12月份下降了1.5m%.今年2月份,经销商决定对该手机以1月份价格的“八折”销售,这样2月份的销售量比今年1月份增加了1.5万台.若今年2月份这种品牌手机的销售额为6400万元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度约为( )(精确到0.1米,参考数据:
,则大楼AB的高度约为( )(精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)

A. 30.6 B. 32.1 C. 37.9 D. 39.4
查看答案和解析>>
科目:初中数学 来源: 题型:
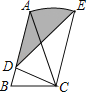
【题目】如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥合家福超市为了吸引顾客,设计了一种促销活动:在三等分的转盘上依次标有“合”,“家”,“福”字样,购物每满200元可以转动转盘1次,转盘停下后,指针所指区域是“福”时,便可得到30元购物券(指针落在分界线上不计次数,可重新转动一次),一个顾客刚好消费400元,并参加促销活动,转了2次转盘.
(1)求出该顾客可能获得购物券的最高金额和最低金额;
(2)请用画树状图法或列表法求出该顾客获购物券金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
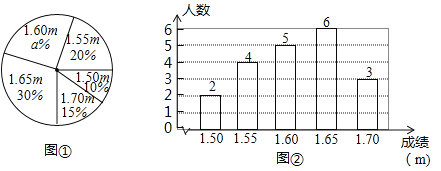
(Ⅰ)图①中![]() 的值为__________;
的值为__________;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定10人能进入复赛,请直接写出初赛成绩为![]() 的运动员能否进入复赛.
的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC=16.点D在边BC上,且点D到边AB和边AC的距离相等.
(1)用直尺和圆规作出点D(不写作法,保留作图痕迹,在图上标注出点D);
(2)求点D到边AB的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com