
分析 (1)根据规律可得出(x-1)(x7+x6+x5+x4+x3+x2+x+1)结果;
(2)由规律得出x的指数为n+1,即可得出答案;
(3)1+2+22+…+234+235的可以写成(2-1)(20+21+22++…+234+235),根据规律计算即可.
解答 解:(1)由规律得:(x-1)(x7+x6+x5+x4+x3+x2+x+1)=x8-1;
(2)(x-1)(xn+xn-1+…+x2+x+1)=xn+1-1;
(3)1+2+22+…+234+235=(2-1)(20+21+22++…+234+235)
=236-1,
故答案为x8-1,xn+1-1.
点评 本题考查了整式的混合运算,明确最后结果的最高指数比第二个括号中的最高指数多1,是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
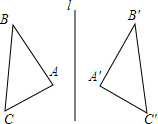 如图,△ABC与△A′B′C′关于直线l对称,若∠A=68°,∠C′=38°,则∠B的度数为( )
如图,△ABC与△A′B′C′关于直线l对称,若∠A=68°,∠C′=38°,则∠B的度数为( )| A. | 38° | B. | 74° | C. | 94° | D. | 68° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com