
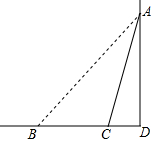
 如图所示,一块广告牌AB顶端固定在一堵墙AD的A点处,与地面夹角∠ABD=45°,由于施工底部断裂掉一段以后,底部落在距离B点8米处的C点,此时与地面夹角∠ACD=75°.求断裂前、后的广告牌AB、AC的长度.
如图所示,一块广告牌AB顶端固定在一堵墙AD的A点处,与地面夹角∠ABD=45°,由于施工底部断裂掉一段以后,底部落在距离B点8米处的C点,此时与地面夹角∠ACD=75°.求断裂前、后的广告牌AB、AC的长度. 分析 过点C作CE⊥AB于E点,解直角三角形即可得到结论.
解答 解: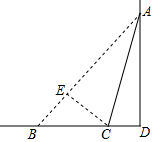 过点C作CE⊥AB于E点,
过点C作CE⊥AB于E点,
在Rt△BCE中sin∠ABD=$\frac{CE}{BC}$,
∴CE=8•sin45°=4$\sqrt{2}$,同理,BE=4$\sqrt{2}$,
∵∠ACD=∠ABD+∠BAC,
∴∠BAC=75°-45°=30°,
在Rt△ACE中,sin∠BAC=$\frac{CE}{AC}$,
∴AC=$\frac{4\sqrt{2}}{sin30°}$=8$\sqrt{2}$,
同理,AE=4$\sqrt{6}$,
∴AB=AE+BE=4$\sqrt{2}$+4$\sqrt{6}$,
答:断裂前的广告牌AB长(4$\sqrt{2}$+4$\sqrt{6}$)米,断裂后的广告牌AC的长度为8$\sqrt{2}$米.
点评 本题考查了解直角三角形的应用,熟练掌握三角函数的定义是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
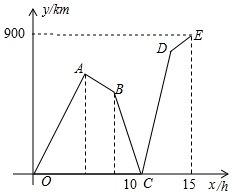 一列快车和一列慢车同时从甲地出发,分别以速度v1、v2(单位:km/h,且v1>2v2)匀速驶向乙地.快车到达乙地后停留了2h,沿原路仍以速度v1匀速返回甲地.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示从慢车出发至慢车到达乙地的过程中,y与x之间的函数关系.根据图象进行以下探究:
一列快车和一列慢车同时从甲地出发,分别以速度v1、v2(单位:km/h,且v1>2v2)匀速驶向乙地.快车到达乙地后停留了2h,沿原路仍以速度v1匀速返回甲地.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示从慢车出发至慢车到达乙地的过程中,y与x之间的函数关系.根据图象进行以下探究:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
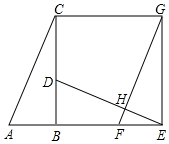 如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.
如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com