
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,BF平分∠ABC,过点C作CF⊥BF于F点,过A作AD⊥BF于D点.AC与BF交于E点,下列四个结论:①BE=2CF;②AD=DF;③AD+DE=![]() BE;④AB+BC=2AE.其中正确结论的序号是( )
BE;④AB+BC=2AE.其中正确结论的序号是( )

A.只有①②③B.只有②③C.只有①②④D.只有①④
【答案】A
【解析】
适当做辅助线,构建三角形.延长CF并交BA延长线于H
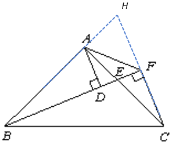
①证明△ABE≌△ACH,得到BE=CH,又可证CH=2CF,故可得BE=2CF
②若要得到AD=DF,则需要证明△ADF为等腰直角三角形,需要证明∠DAF为45°即可
③过E作![]() 交AF于点M,证明△EMF为等腰直角三角形,
交AF于点M,证明△EMF为等腰直角三角形,![]()
![]()
④过E作![]() 于点N,证明
于点N,证明![]() ,得到
,得到![]() ,即可证明④错误.
,即可证明④错误.
①延长BA、CF,交于点H,

∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
![]()
![]()
∴![]()
∵![]()
![]()
∴![]()
∴![]()
②由①知,F为CH中点,又![]() 为直角三角形
为直角三角形
故![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
又BF为![]() 的平分线
的平分线
∴![]()
∴![]()
∴![]()
![]()
在![]() 中,
中,![]()
∴![]()
③过E作![]() 交AF于点M,由②知,CA为∠DAF的平分线
交AF于点M,由②知,CA为∠DAF的平分线
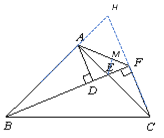
∴![]()
△EMF为等腰直角三角形
∴![]()
∴![]()
④过E作![]() 于点N,可知
于点N,可知![]()
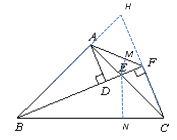
在![]() 中,
中,![]()
∴![]()
即![]() ,而
,而![]()
∴![]()
故![]()
∴![]() ,故④错误,本题答案选A.
,故④错误,本题答案选A.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ABC+![]() .
.

(1)求证:AB=AC;
(2)如图2,点D为AC垂直平分线上一点(点D在AC的右侧),连接BD,∠DBC=30°,∠ABC 的平分线AE交BD于点E;
①求证:△ACD 为等边三角形;
②若AE=nBE,△ABC 的面积记为S△ABC ,△BDC的面积记为S△BDC,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),点P是等腰三角形ABC底边BC上的一动点,过点P作BC的垂线,交直线AB于点Q,交CA的延长线于点R.
(1)试猜想线段AR与AQ的长度之间存在怎样的数量关系?并证明你的猜想.
(2)如图(2),如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,其它条件不变,问(1)中所得的结论还成立吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形ABC中,∠A=110°,求∠B的度数.
例2 等腰三角形ABC中,∠A=40°,求∠B的度数.
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(﹣1,0),B(3,0),C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上求一点P,使△PBC面积为1;
(3)在x轴下方且在抛物线对称轴上,是否存在一点Q,使∠BQC=∠BAC?若存在,求出Q点坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,已知AB与CD不平行,∠ABD=∠ACD,请你添加一个条件:______ .使得加上这个条件后能够推出AB=CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com