练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．先化简$\frac{{x}^{2}-4x+4}{{x}^{2}-2x}$÷（x-$\frac{4}{x}$），然后从0，1，2中任选一个合适的数作为x的值代入求值．

    分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x=1代入计算即可求出值．

    解答 解：$\frac{{x}^{2}-4x+4}{{x}^{2}-2x}$÷（x-$\frac{4}{x}$），
    =$\frac{（x-2）^{2}}{x（x-2）}$÷$\frac{（x+2）（x-2）}{x}$，
    =$\frac{x-2}{x}$×$\frac{x}{（x+2）（x-2）}$，
    =$\frac{1}{x+2}$．
    当x=1时，原式=$\frac{1}{2+1}$=$\frac{1}{3}$．

    点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    5．在平面直角坐标系中点A（4，0）绕点P（x，y）顺时针旋转90°至B（1，m），若1≤m≤3，则P点运动的路径$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=70°，则∠ABD=（　　）
    A．30°B．40°C．50°D．60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如果a，b，c为正整数，且满足a2+b2=c2，那么，a、b、c叫做一组勾股数．
    （1）请你根据勾股数的意思，说明3、4、5是一组勾股数；
    （2）写出一组不同于3、4、5的勾股数12，16，20；
    （3）如果m表示大于1的整数，且a=4m，b=4m2-1，c=4m2+1，请你根据勾股数的定义，说明a、b、c为勾股数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知a与b互为相反数，c与d互为倒数，x的绝对值等于2，求x3-（a+b）2014+（-cd）2015的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

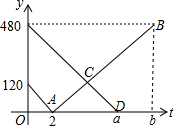    20．甲乙两城市之间有一条公路相连，公路中途穿过丙市，现有两位司机M、N相约各自同时从甲乙两地出发，途中M将一件物品交给N，已知M从甲市到丙市，N从乙市到甲市，N的速度是M的0.75，他们开车距离丙市的距离y（千米）与行驶的时间t（小时）的函数图象如图所示．
    （1）求a的值；
    （2）求AB所在直线的函数解析式及C点的坐标；
    （3）何时他们相距300千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

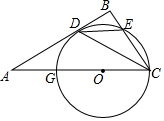    7．如图，点O为Rt△ABC斜边AC上一点，以点O为圆心，OC长为半径的⊙O与AB相切于点D，分别交AC，BC于点G，E．
    （1）求证：$\widehat{DG}$=$\widehat{DE}$．
    （2）若DE∥AC，BE=1，求AG和$\widehat{DG}$的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

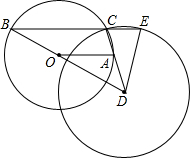    4．如图，在⊙O中，半径OA长为1，弦BC∥OA，射线BO，射线CA交于点D，以点D为圆心，CD为半径的⊙D交BC延长线于点E．
    （1）若BC=$\frac{8}{5}$，求⊙O与⊙D公共弦的长；
    （2）当△ODA为等腰三角形时，求BC的长；
    （3）设BC=x，CE=y，求y关于x的函数关系式，并写出定义域．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5． 如图，第一象限内的点A、B在反比例函数的图象上，点C在y轴上，BC∥x轴，点A的坐标为（2，4），且tan∠ACB=$\frac{2}{3}$
    求：（1）反比例函数的解析式；
    （2）点C的坐标；
    （3）sin∠ABC的值．

    查看答案和解析>>

    同步练习册答案