
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B点,与y轴交于点C(0,﹣3).
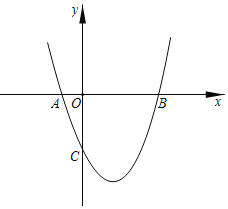
(1)求该抛物线的解析式;
(2)观察图象,直接写出不等式x2+bx+c>0的解集;
(3)设(1)中的抛物线上有一个动点P,点P在该抛物线上滑动且满足S△PAB=8,请求出此时P点的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)x<﹣1或x>3;(3)(1+2![]() ,4)或(1﹣2
,4)或(1﹣2![]() ,4),(1,﹣4),
,4),(1,﹣4),
【解析】
(1)直接把A,C点代入进而求出函数解析式;
(2)直接求出B点坐标进而利用函数图象得出答案;
(3)分点P在x轴上方时,点P在x轴下方时两种情况,分别求解得出答案.
解:(1)把A(﹣1,0)和C(0,﹣3)代入抛物线解析式得:![]() ,
,
解得:![]() ,
,
故抛物线解析式为:y=x2﹣2x﹣3;
(2)当y=0时,0=x2﹣2x﹣3,
则(x﹣3)(x+1)=0,
解得:x1=﹣1,x2=3,
故B(3,0),
则不等式x2+bx+c>0的解集是:x<﹣1或x>3;
(3)设P的纵坐标为|yP|,
∵S△PAB=8,
∴![]() AB|yP|=8,
AB|yP|=8,
∵AB=3+1=4,
∴|yP|=4,
∴yP=±4,
当点P在x轴上方时,∴yP=4,
把yP=4代入解析式得,4=x2﹣2x﹣3,
解得,x=1±2![]() ,
,
∴点P在该抛物线上滑动到(1+2![]() ,4)或(1﹣2
,4)或(1﹣2![]() ,4).
,4).
当点P在x轴下方时,∴yP=﹣4,
把yP=﹣4代入解析式得,﹣4=x2﹣2x﹣3,
解得,x=1,
∴点P在该抛物线上滑动到(1,﹣4),
综上所述:P点坐标为:(1+2![]() ,4)或(1,﹣4)或(1﹣2
,4)或(1,﹣4)或(1﹣2![]() ,4).
,4).


科目:初中数学 来源: 题型:
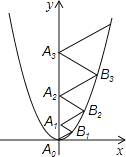
【题目】二次函数y=![]() x2的图象如图所示,点A位于坐标原点,点A1,A2,A3,…,A2019在y轴的正半轴上,点B1,B2,B3,…,B2019在二次函数y=
x2的图象如图所示,点A位于坐标原点,点A1,A2,A3,…,A2019在y轴的正半轴上,点B1,B2,B3,…,B2019在二次函数y=![]() x2位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2018B2019A2019都为等边三角形,则△A2018B2019A2019的边长为_____.
x2位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2018B2019A2019都为等边三角形,则△A2018B2019A2019的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则乙的射击成绩较稳定
C.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.在3张卡片上分别写有实数0,![]() ,
,![]() ,从中随机抽取一张,抽到无理数的概率是
,从中随机抽取一张,抽到无理数的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,BE=EC,将正方形ABCD的边CD沿DE折叠到DF,连接EF、FC、FB,若△DFC的面积为16,则△BEF的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
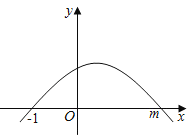
【题目】如图,y=ax2+bx+c的图象经过点(﹣1,0),(m,0);有如下判断:①abc<0;②b>3c;③![]() =1﹣
=1﹣![]() ;④|am+a|=
;④|am+a|=![]() .其中正确的判断有( )
.其中正确的判断有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
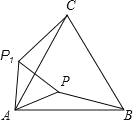
【题目】△ABC 是等边三角形,点 P 在△ABC 内,PA=2,将△PAB 绕点 A 逆时针旋转得到△P1AC,则 P1P 的长等于( )
A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
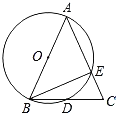
【题目】如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,∠BAC=45°,给出下列四个结论:①∠EBC=22.5°②BD=DC③AE=DC④![]() =2
=2![]() ,其中正确结论有_____(只填序号)
,其中正确结论有_____(只填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com