
【题目】观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30° . 已知楼房高AB约是45m , 根据以上观测数据可求观光塔的高CD是m . 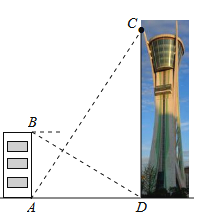
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD. 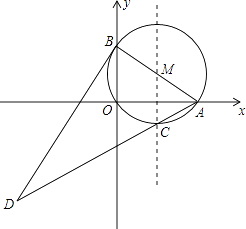
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP﹣AP|最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S= ![]() (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p= ![]() ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5
∴p= ![]() =6
=6
∴S= ![]() =
= ![]() =6
=6
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图,在△ABC中,BC=5,AC=6,AB=9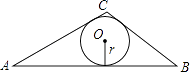
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,小敏、小颖分别画了△ABC和△DEF , 尺寸如图.如果两个三角形的面积分别记作S△ABC、S△DEF , 那么它们的大小关系是( )
A.S△ABC>S△DEF
B.S△ABC<S△DEF
C.S△ABC=S△DEF
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是某市坏城路的一段,AE、BF、CD都是南北方向的街道,其与环城路AC的交叉口分别是A、B、C经测量花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.
(1)求∠ADB的大小;
(2)求B、D之间的距离;
(3)求C、D之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在6×8网格图中,每个小正方形边长均为1,点O和A、B、C三点均为格点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且位似比为1:2;
(2)连接(1)中的AA′,求四边形AA′C′C的周长.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com