
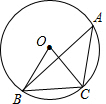
 如图,∠A是⊙O的圆周角,∠OBC=55°,则∠A=35°.
如图,∠A是⊙O的圆周角,∠OBC=55°,则∠A=35°.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
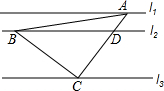 如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )
如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )| A. | $\frac{4\sqrt{2}}{5}$ | B. | $\frac{\sqrt{34}}{5}$ | C. | $\frac{5\sqrt{2}}{8}$ | D. | $\frac{20\sqrt{2}}{23}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
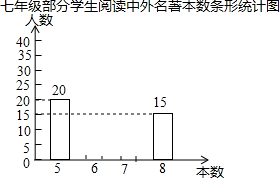 为响应“全民阅读”号召,某校在七年级800名学生中随机抽取100名学生,对该年级学生在2015年全年阅读中外名著的情况进行调查,整理调查结果发现,学生阅读中外名著的本数,最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的条形统计图,其中阅读了6本的人数占被调查人数的30%,根据图中提供的信息,补全条形统计图并估计该校七年级全体学生在2015年全年阅读中外名著的总本数.
为响应“全民阅读”号召,某校在七年级800名学生中随机抽取100名学生,对该年级学生在2015年全年阅读中外名著的情况进行调查,整理调查结果发现,学生阅读中外名著的本数,最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的条形统计图,其中阅读了6本的人数占被调查人数的30%,根据图中提供的信息,补全条形统计图并估计该校七年级全体学生在2015年全年阅读中外名著的总本数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
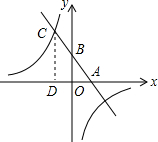 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6.
已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
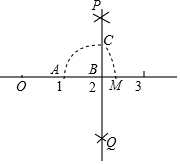 如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )
如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
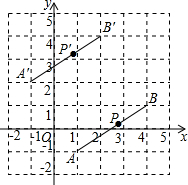 如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A′B′上的对应点P′的坐标为( )
如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A′B′上的对应点P′的坐标为( )| A. | (a-2,b+3) | B. | (a-2,b-3) | C. | (a+2,b+3) | D. | (a+2,b-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com