
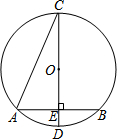
 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=15°,AB=4cm,则⊙O半径为4cm.
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=15°,AB=4cm,则⊙O半径为4cm.  活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
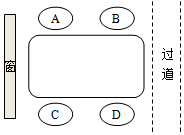 莫菲、隆迪、紫惠和曲代4人一起去火锅店吃火锅,4人在如图所示的四人桌前就座,其中莫菲和紫惠坐在餐桌的同侧,
莫菲、隆迪、紫惠和曲代4人一起去火锅店吃火锅,4人在如图所示的四人桌前就座,其中莫菲和紫惠坐在餐桌的同侧,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
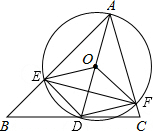 如图,在△ABC中,AB=10$\sqrt{2}$,∠BAC=60°,∠B=45°,点D是BC边上一动点,连接AD,以AD为直径作⊙O交边AB、AC于点E、F,连接OE、OF、DE、DF、EF.
如图,在△ABC中,AB=10$\sqrt{2}$,∠BAC=60°,∠B=45°,点D是BC边上一动点,连接AD,以AD为直径作⊙O交边AB、AC于点E、F,连接OE、OF、DE、DF、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
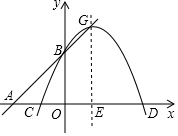 已知二次函数y=ax2-4ax+a2+2(a<0)图象的顶点G在直线AB上,其中
已知二次函数y=ax2-4ax+a2+2(a<0)图象的顶点G在直线AB上,其中查看答案和解析>>
科目:初中数学 来源: 题型:选择题
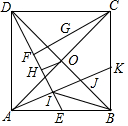 如图,正方形ABCD的边长为2,对角线AC与BC相交于O,E为AB的中点,F为DE的中点,G为CF的中点,OH⊥DE于H,过A作AI⊥DE于I,交BD于J,交BC于K,连接BI,下列结论:①G到AC的距离等于$\frac{\sqrt{2}}{8}$;②OH=$\frac{\sqrt{5}}{5}$;③BK=$\frac{1}{2}$AK;④∠BIJ=45°.其中正确的结论是( )
如图,正方形ABCD的边长为2,对角线AC与BC相交于O,E为AB的中点,F为DE的中点,G为CF的中点,OH⊥DE于H,过A作AI⊥DE于I,交BD于J,交BC于K,连接BI,下列结论:①G到AC的距离等于$\frac{\sqrt{2}}{8}$;②OH=$\frac{\sqrt{5}}{5}$;③BK=$\frac{1}{2}$AK;④∠BIJ=45°.其中正确的结论是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
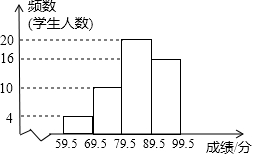 为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如图统计图.
为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如图统计图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com