
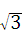 x+4
x+4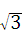 гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЁЯABC=60ЁуЃЌBCгыxжсНЛгкЕуCЃЎ
гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЁЯABC=60ЁуЃЌBCгыxжсНЛгкЕуCЃЎ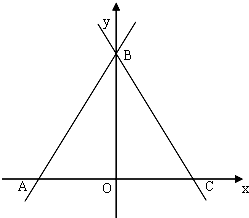
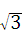 ЉwЃЌ
ЉwЃЌ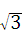 ЃЌ
ЃЌ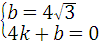 ЃЌ
ЃЌ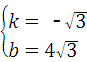 ЃЌ
ЃЌ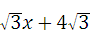 ЃЛЃЈ2ЗжЃЉ
ЃЛЃЈ2ЗжЃЉ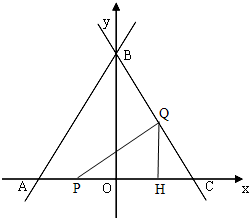
 ЃЌ
ЃЌ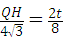 ЃЌ
ЃЌ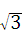 t
t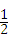 AP•QH=
AP•QH=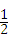 t•
t•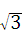 t=
t=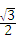 t2Љv0ЃМtЁм4ЉwЃЌЃЈ2ЗжЃЉ
t2Љv0ЃМtЁм4ЉwЃЌЃЈ2ЗжЃЉ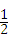 t•Љv8
t•Љv8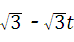 Љw=Љ
Љw=Љ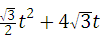 Љv4ЁмtЃМ8ЉwЃЛЃЈ2ЗжЃЉ
Љv4ЁмtЃМ8ЉwЃЛЃЈ2ЗжЃЉ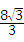 ЃЉЃЎЃЈ4ЗжЃЉНтЮі:
ЃЉЃЎЃЈ4ЗжЃЉНтЮі:


| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
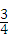 x2+bx+cЃЌЦфЭМЯѓЖдГЦжсЮЊжБЯпx=1ЃЌЧвОЙ§ЕуЃЈ2ЃЌЉ
x2+bx+cЃЌЦфЭМЯѓЖдГЦжсЮЊжБЯпx=1ЃЌЧвОЙ§ЕуЃЈ2ЃЌЉ ЃЉЃЎ
ЃЉЃЎ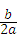 ЃЎ
ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2011ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКкСњНЪЁКкКгЪаОэЃЉЪ§бЇ ЬтаЭЃКНтД№Ьт
ЃЈ2011•КкКгЃЉвбжЊЃКЖўДЮКЏЪ§y=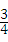 x2+bx+cЃЌЦфЭМЯѓЖдГЦжсЮЊжБЯпx=1ЃЌЧвОЙ§ЕуЃЈ2ЃЌЉ
x2+bx+cЃЌЦфЭМЯѓЖдГЦжсЮЊжБЯпx=1ЃЌЧвОЙ§ЕуЃЈ2ЃЌЉ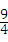 ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉЧѓДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЎ
ЃЈ2ЃЉЩшИУЭМЯѓгыxжсНЛгкBЁЂCСНЕуЃЈBЕудкCЕуЕФзѓВрЃЉЃЌЧыдкДЫЖўДЮКЏЪ§xжсЯТЗНЕФЭМЯѓЩЯШЗЖЈвЛЕуEЃЌЪЙЁїEBCЕФУцЛ§зюДѓЃЌВЂЧѓГізюДѓУцЛ§ЃЎ
зЂЃКЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЖдГЦжсЪЧжБЯпx=Љ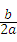 ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК2011ФъГѕжаБЯвЕЩ§бЇПМЪдЃЈКкСњНЪЁКкКгЪаОэЃЉЪ§бЇ ЬтаЭЃКЬюПеЬт
ЃЈ2011?КкКгЃЉвбжЊШ§НЧаЮЯрСкСНБпГЄЗжБ№ЮЊ20cmКЭ30cmЃЌЕкШ§БпЩЯЕФИпЮЊ10cmЃЌдђДЫШ§НЧаЮЕФУцЛ§ЮЊЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com