
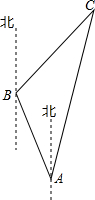
 为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查,一测量船在A岛测得B岛在北偏西30°,C岛在北偏东15°,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离($\sqrt{6}$≈2.45,结果保留到整数)
为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查,一测量船在A岛测得B岛在北偏西30°,C岛在北偏东15°,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离($\sqrt{6}$≈2.45,结果保留到整数) 分析 过点B作BD⊥AC于点D,由等腰直角三角形的性质求出AD的长,再由直角三角形的性质即可得出结论.
解答 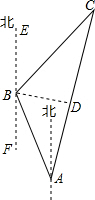 解:由题意知:∠BAC=45°,∠FBA=30°,∠EBC=45°,AB=100海里;
解:由题意知:∠BAC=45°,∠FBA=30°,∠EBC=45°,AB=100海里;
过B点作BD⊥AC于点D,
∵∠BAC=45°,
∴△BAD为等腰直角三角形;
∴BD=AD=50$\sqrt{2}$,∠ABD=45°;
∴∠CBD=180°-30°-45°-45°=60°,
∴∠C=30°;
∴在Rt△BCD中BC=100$\sqrt{2}$≈141海里,CD=50$\sqrt{6}$,
∴AC=AD+CD=50$\sqrt{2}$+50$\sqrt{6}$≈193海里.
点评 本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 方差 | B. | 平均数 | C. | 中位数 | D. | 众数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
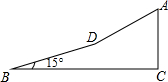 如图,某校八年级(1)班学生利用寒假期间到郊区进行社会实践活动,活动之余,同学们准备攀登附近的一个小山坡,从B点出发,沿坡脚15°的坡面以5千米/时的速度行至D点,用了10分钟,然后沿坡比为1:$\sqrt{3}$的坡面以3千米/时的速度达到山顶A点,用了5分钟,求小山坡的高(即AC的长度)(精确到0.01千米)(sin15°≈0.2588,cos15°≈0.9659,$\sqrt{3}$≈1.732)
如图,某校八年级(1)班学生利用寒假期间到郊区进行社会实践活动,活动之余,同学们准备攀登附近的一个小山坡,从B点出发,沿坡脚15°的坡面以5千米/时的速度行至D点,用了10分钟,然后沿坡比为1:$\sqrt{3}$的坡面以3千米/时的速度达到山顶A点,用了5分钟,求小山坡的高(即AC的长度)(精确到0.01千米)(sin15°≈0.2588,cos15°≈0.9659,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
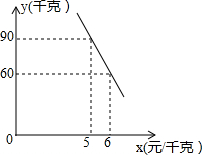 某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.| 蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
| 所付的金额(元) | … | 125 | 300 | 300 | 360 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:用一段长为30m的篱笆围成一边靠墙的矩形菜园,墙长为18m,设菜园的宽AB为xm,面积为Sm2.
如图:用一段长为30m的篱笆围成一边靠墙的矩形菜园,墙长为18m,设菜园的宽AB为xm,面积为Sm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在一面靠墙的空地商用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.
如图,在一面靠墙的空地商用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S平方米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com