
分析 解方程$\frac{x-k}{2}$+$\frac{1}{3}$=$\frac{2k+x}{3}$就可以求出方程的解,这个解的相反数也是方程$\frac{x+k}{3}$=2的解,根据方程的解的定义,把这个解的相反数代入就可以求出k的值.
解答 解:解$\frac{x-k}{2}$+$\frac{1}{3}$=$\frac{2k+x}{3}$,得x=7k-2;
解$\frac{x+k}{3}$=2,得x=6-k,
x的方程$\frac{x-k}{2}$+$\frac{1}{3}$=$\frac{2k+x}{3}$的解与关于x的方程$\frac{x+k}{3}$=2的解互为相反数,得
(7k-2)+(6-k)=0.
解得k=-$\frac{2}{3}$.
点评 本题考查了一元一次方程的解,本题的关键是正确解一元一次方程以及互为相反数的意义.方程的解就是能够使方程左右两边相等的未知数的值.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
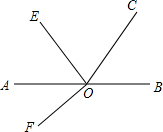 已知O为直线AB上一点,∠BOC=50°,锐角∠AOE在∠A0C内部.如图,过O作OF,使∠EOF为直角,若锐角∠AOE大小变化时,下面两个结论:①∠EOC-∠AOF的值不变;②∠EOC+∠AOF的值不变.其中只有一个正确,请选择正确的结论并说明理由,求出其值.
已知O为直线AB上一点,∠BOC=50°,锐角∠AOE在∠A0C内部.如图,过O作OF,使∠EOF为直角,若锐角∠AOE大小变化时,下面两个结论:①∠EOC-∠AOF的值不变;②∠EOC+∠AOF的值不变.其中只有一个正确,请选择正确的结论并说明理由,求出其值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
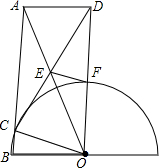 如图.在△AB0中,AB=A0=2B0,以O为圆心,OB为半径的半圆交AB边于点C.△ABO绕点O顺时针旋转得△DCO,DC交AO于点E,DO交半圆于点F,连接AD,EF.
如图.在△AB0中,AB=A0=2B0,以O为圆心,OB为半径的半圆交AB边于点C.△ABO绕点O顺时针旋转得△DCO,DC交AO于点E,DO交半圆于点F,连接AD,EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回,设x秒后两车间的距离为y千米,y关于x的函数关系如图所示.
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回,设x秒后两车间的距离为y千米,y关于x的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,a∥b∥c,AB=3,BC=2,CD=1,那么下列式子中不成立的是( )
如图,a∥b∥c,AB=3,BC=2,CD=1,那么下列式子中不成立的是( )| A. | EC:CG=5:1 | B. | EF:FC=1:1 | C. | EF:FC=3:2 | D. | EF:EC=3:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
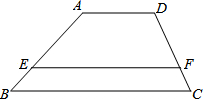 如图,在梯形ABCD中,AD∥BC,AD=3,BC=9,AB=6,CD=4.若EF∥BC,且梯形AEFD与梯形EBCF的周长相等,则EF的长为$\frac{39}{5}$.
如图,在梯形ABCD中,AD∥BC,AD=3,BC=9,AB=6,CD=4.若EF∥BC,且梯形AEFD与梯形EBCF的周长相等,则EF的长为$\frac{39}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com