练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．计算：
    （1）$\sqrt{45}$-$\sqrt{20}$
    （2）$\sqrt{27}$×$\sqrt{50}$÷$\sqrt{6}$．

    分析 （1）先化简题目中的二次根式，然后根据二次根式的减法即可解答本题；
    （2）根据二次根式的乘除法可以解答本题．

    解答 解：（1）$\sqrt{45}$-$\sqrt{20}$
    =$3\sqrt{5}-2\sqrt{5}$
    =$\sqrt{5}$；
    （2）$\sqrt{27}$×$\sqrt{50}$÷$\sqrt{6}$
    =$3\sqrt{3}×5\sqrt{2}×\frac{1}{\sqrt{6}}$
    =15．

    点评 本题考查二次根式的混合运算，解答本题的关键是明确二次根式的混合运算的解答方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

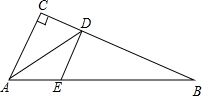    17．如图，在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，点E是AB上任意一点．若CD=5，则DE的最小值等于（　　）
    A．2.5B．4C．5D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．在平面直角坐标系中，O为原点，点A（4，0），点B（0，3），把△ABO绕点B逆时针旋转，得△A′BO′，点A，O旋转后的对应点为A′，O′，记旋转角为α．
    （1）如图①，若α=90°，求AA′的长；
    （2）如图②，若α=120°，求点O′的坐标；
    （3）在（2）的条件下，边OA上 的一点P旋转后的对应点为P′，当O′P+BP′取得最小值时，在图中画出点P的位置，并直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．一次函数y=kx+1的图象必过点（　　）
    A．（0，1）B．（0，-1）C．（1，0）D．（-1，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

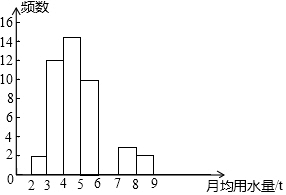    2．小明同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了若干居民的月均用水量（单位：t），并绘制了不完整的样本的频数分布表的频数分布直方图（如图）
    根据上述图表回答下列问题：
    月均用水量（单位：t）频数百分比
    2≤x＜320.04
    3≤x＜4120.24
    4≤x＜5150.3
    5≤x＜6100.2
    6≤x＜760.12
    7≤x＜830.06
    8≤x＜920.04
    （1）小明同学共调查了多少户居民的月均用水量；
    （2）请根据题中已有的信息补全频数分布表和频数分布直方图；
    （3）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你通过样本估计总体中的等用水量家庭大约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．解方程组$\left\{\begin{array}{l}{2（x-3）+3y=11}\\{\frac{x-3}{2}-2y=0}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．观察下列图形：它们是按一定的规律排列，依照此规律第n个图形共有（　　）个五角星．
    A．1+nB．1+2nC．2+nD．1+3n

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

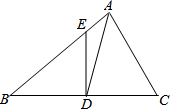    16．如图，在△ABC中，∠B=35°，∠C=65°，AD平分∠BAC，过点D作BC的垂线，交AB于点E，求∠ADE的度数．请完成剩下的解答过程．
    解：∵∠BAC+∠B+∠C=180°，且∠B=35°，∠C=65°
    ∴∠BAC=180°-∠B-∠C=180°-35°-65°=80°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

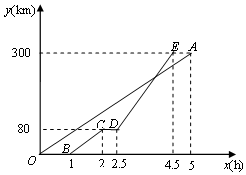    17．甲、乙两地相距300km，一辆货车和一辆轿车先后从甲地出发向乙地．如图，线段OA表示货车离甲地距离y（km）与时间x（h）之间的函数关系，折线BCDE表示轿车离甲地距离y（km）与时间x（h）之间的函数关系．请根据图象，解答下列问题：
    （1）线段CD表示轿车在途中停留了0.5h；
    （2）货车的平均速度是60km/h；
    （3）求线段DE对应的函数解析式．

    查看答案和解析>>

    同步练习册答案