
 如图,有以下五个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5,⑤∠B+∠BAD=180°,其中能判断AB∥CD的条件有( )个.
如图,有以下五个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5,⑤∠B+∠BAD=180°,其中能判断AB∥CD的条件有( )个.| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
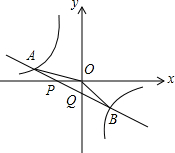 如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB.给出下列结论:
如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m)、B(1,n)两点,连接OA、OB.给出下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一直线与两坐标轴的正半轴分别交于A、B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )
如图,一直线与两坐标轴的正半轴分别交于A、B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )| A. | y=x+10 | B. | y=-x+10 | C. | y=x+20 | D. | y=-x+20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
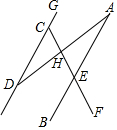 如图,下列条件不能判定AB∥CD的是( )
如图,下列条件不能判定AB∥CD的是( )| A. | ∠BAD=∠ADG | B. | ∠GCE=∠AEF | C. | ∠GDH+∠DHF=180° | D. | ∠FEB+∠GCE=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
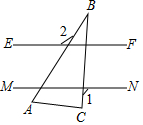 把含有30°的直角三角板(∠ABC=30°)如图放置,若EF∥MN,∠1=100°,则∠2的度数为( )
把含有30°的直角三角板(∠ABC=30°)如图放置,若EF∥MN,∠1=100°,则∠2的度数为( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.3945×104 | B. | 13.945×105 | C. | 1.3945×106 | D. | 1.3945×108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com