
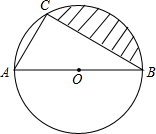
 (2013•青岛)如图,AB是⊙O的直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是
(2013•青岛)如图,AB是⊙O的直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是| 4π |
| 3 |
| 3 |
| 4π |
| 3 |
| 3 |
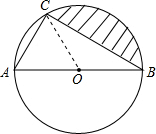 解:如图,连接OC.
解:如图,连接OC.| AB2-AC2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 3 |
| 120π×22 |
| 360 |
| 3 |
| 4π |
| 3 |
| 3 |
| 4π |
| 3 |
| 3 |


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:
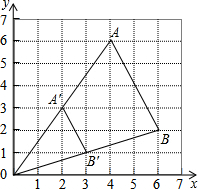 (2013•青岛)如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )
(2013•青岛)如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )查看答案和解析>>
科目:初中数学 来源: 题型:
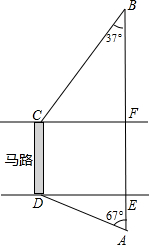 (2013•青岛)如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°.
(2013•青岛)如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直,马路宽20米,A,B相距62米,∠A=67°,∠B=37°.| 12 |
| 13 |
| 5 |
| 13 |
| 12 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com