
【题目】在等腰![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的高,点
边上的高,点![]() 在
在![]() 的外部且
的外部且![]() ,
,![]() ,连接
,连接![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)如图①,当![]() 时,求证:
时,求证:![]() ;
;
(2)如图②,当![]() 时,求
时,求![]() 的度数;
的度数;
(3)如图③,当![]() 时,求证:
时,求证:![]() .
.
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据等腰三角形三线合一的性质,可得AE垂直平分BC,F为垂直平分线AE上点,即可得出结论;
(2)根据(1)的结论可得AE平分∠BAC,∠BAF=20°,由AB=AC=AD,推出
![]() ,根据外角性质可得
,根据外角性质可得![]() 计算即可;
计算即可;
(3)在CF上截取CM=DF,连接AM,证明△ACM≌△ADF(SAS),进而证得△AFM为等边三角形即可.
(1)证明:∵AE为等腰△ABC底边BC上的高线,AB=AC,
![]() ,∠AEB=∠AEC=90°,BE=CE,
,∠AEB=∠AEC=90°,BE=CE,
∴AE垂直平分BE,F在AE上,
![]() ;
;
(2) ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
由(1)知,AE平分∠BAC,
![]() ,
,
![]() ,
,
故答案为:60°;
(3) 在CF上截取CM=DF,连接AM,
由(1)可知,∠ABC=∠ACB,∠ABE=∠ACE,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在△ACM和△ADF中,
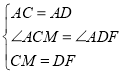
∴△ACM≌△ADF(SAS),
![]() ,
,
![]() ,
,
∴△AFM为等边三角形,
![]() ,
,
![]() .
.


 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广,为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写大赛”![]() 为了解本次大赛的成绩,校团委随机抽取了其中若干名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
为了解本次大赛的成绩,校团委随机抽取了其中若干名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩 | 频数 | 频率 |
| 10 |
|
| 30 |
|
| 40 | n |
| m |
|
| 50 |
|
a | 1 |
请根据所给信息,解答下列问题:
![]() ______,
______,![]() ______,
______,![]() ______;
______;
![]() 补全频数直方图;
补全频数直方图;
![]() 这若干名学生成绩的中位数会落在______分数段;
这若干名学生成绩的中位数会落在______分数段;
![]() 若成绩在90分以上
若成绩在90分以上![]() 包括90分
包括90分![]() 的为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
的为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
A. 有两边和其中一边的对角对应相等的两个三角形全等
B. 两条平行直线被第三条直线所截,则一组同旁内角的平分线互相垂直
C. 三角形的一个外角等于两个内角的和
D. 等边三角形既是中心对称图形,又是轴对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某农户发展养禽业,准备利用现有的34米长的篱笆靠墙AB(墙长为25米)围成一个面积为120平方米的长方形养鸡场,这个养鸡场的长和宽各是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为m的正方形面积为12,则下列关于m的说法中:①m2是有理数;②m的值满足m2﹣12=0;③m满足不等式组![]() ;④m是12的算术平方根. 正确有几个( )
;④m是12的算术平方根. 正确有几个( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.

(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四点A、B、C、D.
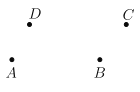
(1)用圆规和无刻度的直尺按下列要求与步骤画出图形:
①画直线AB.
②画射线DC.
③延长线段DA至点E,使![]() .(保留作图痕迹)
.(保留作图痕迹)
④画一点P,使点P既在直线AB上,又在线段CE上.
(2)在(1)中所画图形中,若![]() cm,
cm,![]() cm,点F为线段DE的中点,求AF的长.
cm,点F为线段DE的中点,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com