解答: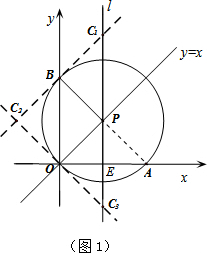
解:(1)
,OA=2,OB=2; …(3分)
(2)符合条件的点C有3个,如图1.
连接PA,∵∠AOB=90°,由圆周角定理可知,AB为圆的直径,点A、P、B共线.
∵圆心P在直线y=x上,∴∠POA=∠POB=45°,
又∵PO=PA=PB,∴△POB与△POA均为等腰直角三角形.
设动直线l与x轴交于点E,则有E(t,0),P(t,t),B(0,2t).
∵OBPC
1为平行四边形,∴C
1P=OB=2t,C
1E=C
1P+PE=2t+t=3t,
∴C
1(t,3t);
同理可求得:C
3(t,-t);
∵OPBC
2为平行四边形,且PB=PO,∠OPB=90°,
∴?OPBC
2为正方形,其对角线OB位于y轴上,则点P与点C
2关于x轴对称,
∴C
2(-t,t);
∴符合条件的点C有3个,分别为C
1(t,3t)、C
2(-t,t)、C
3(t,-t);…(7分)
(3)△DAC是等腰直角三角形.理由如下:
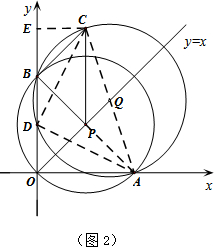
当点C在第一象限时,如图2,连接DA、DC、PA、AC.
由(2)可知,点C的坐标为(t,3t),由点P坐标为(t,t),点A坐标为(2t,0),点B坐标为(0,2t),
可知OA=OB=2t,△OAB是等腰直角三角形,
又PO=PB,进而可得△OPB也是等腰直角三角形,则∠POB=∠PBO=45°.
∵∠AOB=90°,∴AB为⊙P的直径,∴A、P、B三点共线,
又∵BC∥OP,∴∠CBE=∠POB=45°,
∴∠ABC=180°-∠CBE-∠PBO=90°,

∴AC为⊙Q的直径,∴DA⊥DC…(9分)
∴∠CDE+∠ADO=90°
过点C作CE⊥y轴于点E,则有∠DCE+∠CDE=90°,∴∠ADO=∠DCE,
∴Rt△DCE∽Rt△ADO,
∴
=,即
=,
解得OD=t或OD=2t
依题意,点D与点B不重合,∴舍去OD=2t,只取OD=t,
∴
=1,即相似比为1,此时两个三角形全等,则DC=AD,
∴△DAC是等腰直角三角形.…(11分)
当点C在第二象限时,如图3,同上可证△DAC也是等腰直角三角形. …(12分)
综上所述,当点C在直线y=x上方时,△DAC必为等腰直角三角形.…(13分)

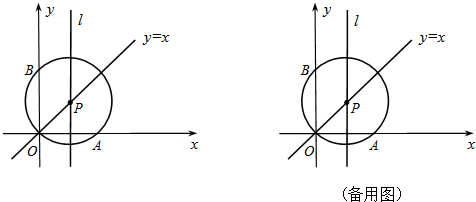
 解:(1)
解:(1)



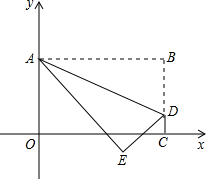 (2013•晋江市)将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(2013•晋江市)将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.