
����Ŀ��ij��˾����һ�ֽ�����Ʒ���г��Ϻ��ܻ�ӭ���ù�˾ÿ��IJ���Ϊ6��������ڹ��ں��������г�ȫ�����ۣ����ڹ������ۣ�ƽ��ÿ����Ʒ������y1��Ԫ�������������x��������ĺ�����ϵʽΪy1=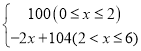 �����ڹ������ۣ�ƽ��ÿ����Ʒ������Ϊy2=84Ԫ��
�����ڹ������ۣ�ƽ��ÿ����Ʒ������Ϊy2=84Ԫ��
��1����ù�˾ÿ���ڹ��ں������۵�������w����Ԫ�������������x��������ĺ�����ϵʽ����ָ��x��ȡֵ��Χ��
��2���ù�˾ÿ���ڹ��ڹ�����������Ϊ����ʱ����ʹ��˾ÿ���������������ֵ�Ƕ��٣�
��3���ù�˾�ƻ��ӹ������۵�ÿ����Ʒ�о��2m��1��m��4��Ԫ��ϣ�����̣��ӹ������۵�ÿ����Ʒ�о��mԪ��ϣ�����̣��ҹ������۲�����4���������ʱ���ڹ������۵�����������ֵΪ520��Ԫ����m��ֵ��
���𰸡���1��w=![]() ����2�����ù�˾ÿ��Ĺ���������Ϊ5���������������Ϊ1���ʱ����ʹ��˾ÿ���������������ֵ��554��Ԫ����3��m=2
����2�����ù�˾ÿ��Ĺ���������Ϊ5���������������Ϊ1���ʱ����ʹ��˾ÿ���������������ֵ��554��Ԫ����3��m=2
��������
��1�����������ÿ����������Լ���������ֶκ�������ʽ������ɵý⣻
��2����ϣ�1���ֱ����ֶ������������ֵ�����ó����ֵ���ɣ�
��3���ù�˾�ƻ��ڹ������۲�����4��������ù�˾ÿ��������Ϊ6�������ù�˾ÿ���ڹ������۵ļ���x�ķ�ΧΪ��0��x��2����������w��=��100-2m��x����84-m����6-x��=��16-m��x��504-6m������m��ȡֵ��Χ��x��ȡֵ��Χ��һ�κ��������ʣ�������������Ϊ520��Ԫ���ɷ�����ã�
�⣺��1��w=y1x��84��6-x����
��0��x��2ʱ��w=100x��84��6-x��=16x��504��
��2��x��6ʱ��w=x��-2x��104����84��6-x��=-2x2��20x��504��
��w=![]() ��
��
��2����0��x��2ʱ��w=16x��504��
��k =16��0����x=2ʱ��w=16x��504�����ֵΪ536��
��2��x��6ʱ��w=-2x2��20x��504=-2��x-5��2��554��
��a=-2��0������x=5ʱȡ���ֵ554��
��554��536�����Ե�x=5ʱȡ���ֵ554��
�������ù�˾ÿ��Ĺ���������Ϊ5���������������Ϊ1���ʱ����ʹ��˾ÿ���������������ֵ��554��Ԫ��
��3�����ù�˾�ƻ��ڹ������۲�����4�������6-x��4����x��2��
���ù�˾ÿ���ڹ������۵ļ���x�ķ�ΧΪ��0��x��2��
��������w��=��100-2m��x����84-m����6-x��=��16-m��x��504-6m��
��1��m��4����16-m��0����x=2ʱ��w��ȡ�����ֵ��
������ã�2��16-m����504-6m=536-8m=520����ã�m=2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһֱ������ϵ�У�������C1��y��ax2��2x��3��������C2��y��x2+mx+n����y��Գƣ�C2��x�ύ��A��B���㣬���е�A�ڵ�B����࣮
��1����������C1��C2�ĺ�������ʽ��
��2����A��B��������ꣻ
��3����������C1���Ƿ����һ��P����������C2���Ƿ����һ��Q��ʹ����ABΪ�ߣ�����A��B��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ����P��Q��������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2+2x+c��y�ύ�ڵ�A����x�ύ�ڵ�B��3��0����C����1��0�����㣮
��1����ֱ��AB�������ߵı���ʽ��
��2������FΪֱ��AB�Ϸ���������һ���㣨����A��B�غϣ�������F��FP//x�ύֱ��AB�ڵ�P������F��FR//y�ύֱ��AB�ڵ�R����PR�����ֵ��
��3��������BA���ŵ�B��ʱ����ת90��õ�����BM����E������BM�˶��������B�غϣ�����BC��BEΪ�ڱ���ƽ���ı���BCDE����HΪDE���϶��㣬����CH����ֱ��д��CH+![]() HE����Сֵ��
HE����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
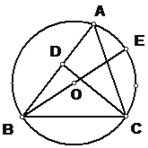
����Ŀ����֪����ͼ��BE�ǡ�ABC�����ԲO��ֱ����CD�ǡ�ABC�ĸߣ�
��1����֤��AC��BC��BE��CD��
��2����֪CD��6��AD��3��BD��8�����O��ֱ��BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ӱ�죬ij���߲˵ļ۸�������ǣ���ԭ�۵�1.5����ͬ����48Ԫ�����߲˱�ԭ������2ǧ�ˣ�
��1���������߲˵�ԭ����ÿǧ�˶���Ԫ��
��2��������ȡ���Ӳɹ����������������ȶ��ִ�ʩ�������ؼۣ������ϰ��յ���������߲˵����ļ������µ�����ÿǧ��10Ԫ��Ϊÿǧ��6.4Ԫ����ƽ��ÿ���µ��İٷ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
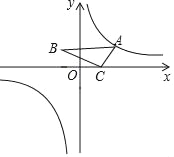
����Ŀ����ͼ��OΪ����ԭ�㣬��C������Ϊ��1��0������ACB=90�㣬��B=30��������A�ڷ���������y=![]() ��ͼ�����˶�ʱ����B�ں���_____���������ʽ����ͼ�����˶���
��ͼ�����˶�ʱ����B�ں���_____���������ʽ����ͼ�����˶���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D��E�ֱ��ǡ�ABC�ı�AB��AC���е㣬H��G�DZ�BC�ϵĵ㣬��HG=![]() BC��S��ABC =12����ͼ����Ӱ���ֵ����Ϊ( )
BC��S��ABC =12����ͼ����Ӱ���ֵ����Ϊ( )
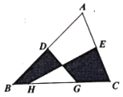
A.6B.4C.3D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
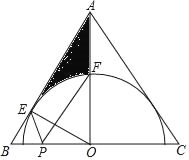
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��AO��BC�ڵ�O��OE��AB�ڵ�E���Ե�OΪԲ�ģ�OEΪ�뾶����Բ����AO�ڵ�F��
��1����֤��AC����O�����ߣ�
��2������F��OA���е㣬OE��3����ͼ����Ӱ���ֵ������
��3���ڣ�2���������£���P��BC���ϵĶ��㣬��PE+PFȡ��Сֵʱ��ֱ��д��BP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�
��![]() ��
��![]() ��
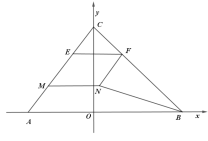
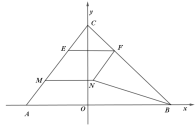
��![]() ��E��MΪ�߶�AC���������غϵĶ��㣨��E�ڵ�M�Ϸ����Ҿ�����˵��غϣ���
��E��MΪ�߶�AC���������غϵĶ��㣨��E�ڵ�M�Ϸ����Ҿ�����˵��غϣ���![]() ����BC���ڵ�F���ı���EMNFΪƽ���ı��Σ�����BN.
����BC���ڵ�F���ı���EMNFΪƽ���ı��Σ�����BN.
��1����ֱ��AC��ֱ��BC�Ľ���ʽ��
��2�������F�ĺ�����Ϊx����M��������Ϊy�����ı���EMNFΪ����ʱ������y����x�ĺ�������ʽ����Ӧx��ȡֵ��Χ��
��3���������![]() Ϊ����������ʱ��
Ϊ����������ʱ��![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com