练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．已知一个等腰三角形的顶角为30°，则它的一个底角等于75°．

    分析 已知明确给出等腰三角形的顶角是30°，根据等腰三角形的性质及三角形的内角和定理易求得底角的度数．

    解答 解：∵等腰三角形的顶角是30°，
    ∴这个等腰三角形的一个底角=$\frac{1}{2}$（180°-30°）=75°．
    故答案为75°．

    点评 此题考查了等腰三角形的性质及三角形内角和定理；此题很简单，解答此题的关键是熟知三角形内角和定理及等腰三角形的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．计算：
    （1）（+9）-（+10）+（-2）-（-8）+3；
    （2）（-12）×（-2$\frac{1}{3}$）×（-$\frac{2}{7}$）；
    （3）-3×$\frac{6}{11}$-2×（-$\frac{6}{11}$）+10×（-$\frac{6}{11}$）；
    （4）-0.5+（-15）-（-17）-|-12|；
    （5）（-$\frac{34}{13}$）×（-$\frac{16}{7}$）×0×$\frac{4}{3}$；
    （6）（$\frac{1}{2}$+$\frac{5}{6}$-$\frac{7}{12}$）×（-36）；
    （7）5×（-1）-（-4）×（-$\frac{1}{4}$）；         
    （8）（-19$\frac{18}{19}$）×15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．将抛物线y=-$\frac{1}{2}$x2向左平移3个单位，再向上平移2个单位．
    （1）写出平移后的抛物线的函数关系式．
    （2）若平移后的抛物线的顶点为A，与x轴的两个交点分别是B、C，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．在下列数：π，0.3，$\sqrt{2}$，-1$\frac{1}{17}$，1.$\stackrel{•}{4}$，0.101001000100001中，无理数有2个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

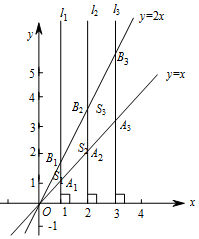    9．如图，直线l1⊥x轴于点（1，0），直线l2⊥x轴于点（2，0），直线l3⊥x轴于点（3，0），…，直线ln⊥x轴于点（n，0）（其中n为正整数）．函数y=x的图象与直线l1，l2，l3，…，ln分别交于点A1，A2，A3，…，An；函数y=2x的图象与直线l1，l2，l3，…，ln分别交于点B1，B2，B3，…，Bn，如果△OA1B1的面积记作S1，四边形A1A2B2B1的面积记作S2，四边形A2A3B3B2的面积记作S3，…，四边形An-1AnBnBn-1的面积记作Sn，那么S2015=$\frac{4031}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

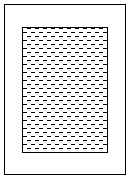    19．如图，用一张高为30cm，宽为20cm的长方形打印纸打印文档，如果左、右的页边距都为xcm，上、下页边距比左、右页边距多1cm．
    （1）请用含x的代数式表示中间打印部分的面积．（结果需化简）
    （2）当x=2时，中间打印部分的面积是多少平方厘米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

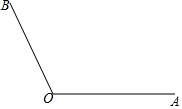    6．如图，已知∠AOB=120°．点C在∠AOB的内部，且∠BOC=30°；OP是∠AOB的角平分线．
    （1）作∠BOC；
    （2）尺规作图：作∠AOB的角平分线OP；（不写作法，保留作图痕迹．）
    （3）如果射线OC、OA分别表示从点O出发的正北、正东两个方向，那么射线OB表示北偏西30°方向；
    （4）在图中找出一个与∠AOP互余的角是∠BOC与∠COP；
    （5）在图中找出所有与∠AOB互补的角是∠AOP与∠BOP．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．计算：（$\sqrt{75}$-$\frac{\sqrt{48}}{\sqrt{4}}$）×$\sqrt{27}$的结果是27．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

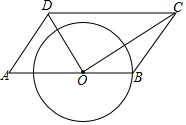    4．如图，平行四边形ABCD中，O为AB上的一点，连接OD、OC，以O为圆心，OB为半径画圆，分别交OD，OC于点P，Q，若OB=2，OD=3，∠ADO=∠A，$\widehat{PQ}$=π，判断直线DC与⊙O的位置关系，并说明理由．

    查看答案和解析>>

    同步练习册答案