
求证:(1)∠APD=∠BPD ;
(2)PA·PB=PC2+AC·CB.
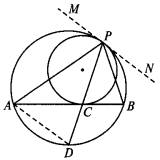
| (1)过点P作两圆的公切线MN.
∵ MN与AB均为小圆的公切线,∴ ∠NPC=∠BCP. ∵ ∠NPC=∠NPB+∠BPC,∠BCP=∠PAC+∠APC, 又∠NPB=∠PAB=∠PAC,∴ ∠NPB+∠BPC=∠PAC+∠APC. ∴ ∠BPC=∠APC,即∠BPD =∠APD. (2)连结AD.由(1)知,∠DPA=∠BPC, 又∵ ∠ADP=∠CBP,∴ △PDA∽△PBC, ∴ 即PA·PB=PC·PD. ∵ PA·PB=PC·PD=(PC+CD)·PC=PC2+CD·PC, 又PC·CD=AC·BC,∴ PA·PB=PC2+AC·BC.
|
| (1)因为∠PAC+∠APC=∠PCB=∠NPB+∠CPB,所以只要证明∠PAC=∠NPB即可.
(2)要证明PA·PB=PC2+AC·CB,根据相交弦定理,得AC·BC=PC·CD,即证PA·PB=PC2+PC·CD=PC(PC+CD)=PC·PD.只需证△PDA∽△PBC即可. 两圆相切时,常作公切线(内切时,常作外公切线;外切时,常作内公切线),两圆的公切线使两圆有公共的弦切角或相等的弦切角,从而把两个圆中的角联系起来.
|


科目:初中数学 来源: 题型:
 已知;如图,两圆内切于点P,大圆的弦AB切小圆于点C,PC的延长线交大圆于点D.
已知;如图,两圆内切于点P,大圆的弦AB切小圆于点C,PC的延长线交大圆于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知;如图,两圆内切于点P,大圆的弦AB切小圆于点C,PC的延长线交大圆于点D.
已知;如图,两圆内切于点P,大圆的弦AB切小圆于点C,PC的延长线交大圆于点D.查看答案和解析>>
科目:初中数学 来源:2000年全国中考数学试题汇编《图形的相似》(03)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2000年全国中考数学试题汇编《圆》(07)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2000年天津市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com