
| ∠BDA | ∠CED | |
| 第一次测量结果 | ||
| 第二次测量结果 |
 =
= ,
,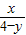 =
=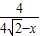 ,
,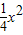 -
-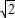 x+4(0<x<4
x+4(0<x<4 ).
).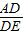 =
=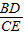 =1,
=1,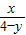 =1,
=1,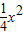 -
- x+4)=x,
x+4)=x, -4,x2=0(舍去),
-4,x2=0(舍去),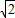 -4;
-4; BC=2
BC=2 ;
; -4或2
-4或2 时,△ADE能成为等腰三角形.
时,△ADE能成为等腰三角形.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com