
分析 (1)求出三组对应边的比,看看是否相等即可;(2)思路雷同;
(3)先根据坐标与图形,分别计算出两三角形三边的长,然后根据三角形相似的判定即可得到△AOB∽△A1OB1.
解答 解:(1)∵△ABC的三边长分别为1,$\sqrt{2}$,$\sqrt{3}$,△DEF的三边长分别为$\sqrt{6}$,$\sqrt{2}$,1;
∴$\frac{1}{1}=\frac{\sqrt{2}}{\sqrt{2}}≠\frac{\sqrt{3}}{\sqrt{6}}$,
∴△ABC与△DEF不相似,
故答案为不相似;
(2)△ABC中,AB:AC:BC=4:3:2,△A1B1C1中,A1B1:A1C1:B1C1=3:2:4,
∴$\frac{AB}{{B}_{1}{C}_{1}}=\frac{AC}{{A}_{1}{B}_{1}}=\frac{BC}{{A}_{1}{C}_{1}}$,
∴△ABC与△A1B1C1相似,
故答案为相似;
(3)在平面直角坐标系中,A(2,0),B(1,2),A1(0,-4),B1(4,-2),
∴AO=2,AB=$\sqrt{5}$,A1B1=2$\sqrt{5}$,OB=$\sqrt{5}$,OA1=4,OB1=2$\sqrt{5}$,A1B1=2$\sqrt{5}$,
∴$\frac{OA}{O{A}_{1}}=\frac{OB}{O{B}_{1}}=\frac{AB}{{A}_{1}{B}_{1}}$=$\frac{1}{2}$,
∴△AOB∽△A1OB1.
故答案为相似.
点评 本题考查了对相似三角形的判定的应用,注意:相似三角形的判定定理之一是:有三组对应边的比相等的两个三角形相似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是一名学生推铅球时,铅球运行高度y(m)与水平距离x(m)之间的函数图象,铅球推出4m时达到最高点,最高点到地面的距离为3m,铅球推出时高度为1.5m,则铅球推出的最大距离为9.7m.(结果精确到0.1米)
如图是一名学生推铅球时,铅球运行高度y(m)与水平距离x(m)之间的函数图象,铅球推出4m时达到最高点,最高点到地面的距离为3m,铅球推出时高度为1.5m,则铅球推出的最大距离为9.7m.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
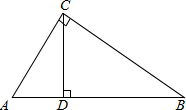 如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.
如图,在Rt△ABC中,CD是斜边AB上的高线,试猜想线段AC,AB,CD,BC是否对应成比例?如果对应成比例,请写出这个比例式,并进行验证;如果不能,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某生活小区的居民筹集资金1600元,计划在一块上,下两底分别为10m,20m的梯形空地种植花木.
某生活小区的居民筹集资金1600元,计划在一块上,下两底分别为10m,20m的梯形空地种植花木.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com