
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{5}{4}$ |
分析 根据直角三角形的周长和勾股定理,可求得两直角边的长以及长的乘积,由此可求出这个三角形的面积.
解答 解:设两直角边分别为a,b,斜边为c,
可得:$\left\{\begin{array}{l}{a+b+c=4+\sqrt{26}}\\{{a}^{2}+{b}^{2}={4}^{2}}\end{array}\right.$,
∴a+b=$\sqrt{26}$,
∴a2+2ab+b2=26,
∴2ab=10,
∴ab=5,
所以三角形的面积是$\frac{5}{2}$,
故选C.
点评 此题考查二次根式的应用,在解题过程中,应了解直角三角形的一些特殊性质,在进行求解的时候使问题变得简单.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
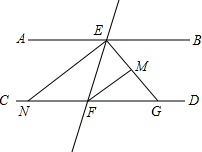 如图,AB∥CD,若EG平分∠BEF,FM平分∠EFD交EG于M,EN平分∠AEF,则与∠FEM互余的角有( )
如图,AB∥CD,若EG平分∠BEF,FM平分∠EFD交EG于M,EN平分∠AEF,则与∠FEM互余的角有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
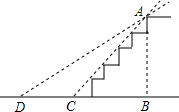 某公园在一个斜坡上计划修建台阶,以方便游客,已知斜坡的高AB=12米,斜坡的坡角∠ACB=45°,后来考虑到有老年人的行走方便,决定将坡角改为30°(即∠ADB=30°),请求出CD的长度(精确到0.1米,其中$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某公园在一个斜坡上计划修建台阶,以方便游客,已知斜坡的高AB=12米,斜坡的坡角∠ACB=45°,后来考虑到有老年人的行走方便,决定将坡角改为30°(即∠ADB=30°),请求出CD的长度(精确到0.1米,其中$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com