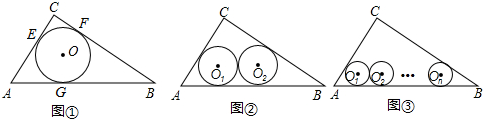
(Ⅰ)(1)证明:在图①中,连接OE,OF,OA.
∵⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.
∴OF⊥BC,OE⊥AC,∠ACB=90°,
∴四边形CEOF是矩形,
又∵EO=OF,
∴四边形CEOF是正方形,
CE=CF=r
1.
又∵AG=AE=3-r
1,BG=BF=4-r
1,
AG+BG=5,
∴(3-r
1)+(4-r
1)=5.
即r
1=1.
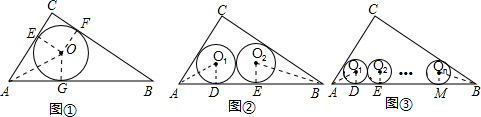
(2)解:连接OG,在Rt△AOG中,
∵r
1=1,AG=3-r
1=2,
tan∠OAG=
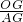
=

;
(Ⅱ)(1)解:连接O
1A、O
2B,作O
1D⊥AB交于点D、O
2E⊥AB交于点E,AO
1、BO
2分别平分∠CAB、∠ABC.
由tan∠OAG=

,知tan∠O
1AD=

,
同理可得:tan∠O
2BE=
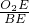
=

,
∴AD=2r
2,DE=2r
2,BE=3r
2.
∵AD+DE+BE=5,
r
2=

;
(2)解:如图③,连接O
1A、O
nB,作O
1D⊥AB交于点D、O
2E⊥AB交于点E、…、O
nM⊥AB交于点M.
则AO
1、BO
n分别平分∠CAB、∠ABC.
tan∠O
1AD=

,tan∠O
nBM=

,
AD=2r
n,DE=2r
n,…,MB=3r
n,
又∵AD+DE+…+MB=5,
2r
n+2r
n+…+3r
n=5,
(2n+3)r
n=5,
r
n=
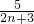
.
分析:(Ⅰ)(1)根据切线的性质以及正方形的判定得出四边形CEOF是正方形,进而得出CE=CF=r
1,再利用切线长定理求出即可;
(2)在Rt△AOG中,根据r
1=1,AG=3-r
1=2,求出tan∠OAG的值即可;
(Ⅱ)(1)由tan∠OAG=

,知tan∠O
1AD=

,同理可得:tan∠O
2BE=
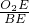
=

,进而得出AD=2r
2,DE=2r
2,BE=3r
2,即可求出r
2=

;
(2)根据(1)中所求可以得出AD=2r
n,DE=2r
n,…,MB=3r
n,得到2r
n+2r
n+…+3r
n=5,求出即可.
点评:此题主要考查了切线长定理以及锐角三角函数关系以及相切两圆的性质,根据已知得出tan∠O
1AD=

,tan∠O
2BE=
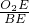
=

是解题关键.


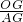 =
= ;
;  ,知tan∠O1AD=
,知tan∠O1AD= ,
,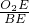 =
= ,
, ;
; ,tan∠OnBM=
,tan∠OnBM= ,
,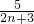 .
. ,知tan∠O1AD=
,知tan∠O1AD= ,同理可得:tan∠O2BE=
,同理可得:tan∠O2BE=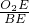 =
= ,进而得出AD=2r2,DE=2r2,BE=3r2,即可求出r2=
,进而得出AD=2r2,DE=2r2,BE=3r2,即可求出r2= ;
; ,tan∠O2BE=
,tan∠O2BE=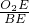 =
= 是解题关键.
是解题关键. 
