
分析 (1)利用乘法法则,分子和分子相乘,分母和分母相乘,利用平方差公式即可求解;
(2)逆用积的乘方法则化成=[(3+$\sqrt{10}$)(3-$\sqrt{10}$)]100•(3-$\sqrt{10}$)的形式,然后利用平方差公式即可求解;
(3)逆用平方差公式即可求解;
(4)首先化简二次根式,然后合并同类二次根式即可;
(5)首先分母有理化,利用同分母的分式的加法即可求解.
解答 解:(1)原式=$\frac{(1-\sqrt{2})(1+\sqrt{2})}{4}$=$\frac{1-2}{4}$=-$\frac{1}{4}$;
(2)原式=[(3+$\sqrt{10}$)(3-$\sqrt{10}$)]100•(3-$\sqrt{10}$)=(-1)100•(3-$\sqrt{10}$)=3-$\sqrt{10}$;
(3)原式=[($\sqrt{a}$+$\sqrt{b}$)+($\sqrt{a}$-$\sqrt{b}$)][($\sqrt{a}$+$\sqrt{b}$)-($\sqrt{a}$-$\sqrt{b}$)]=2$\sqrt{a}$•2$\sqrt{b}$=4$\sqrt{ab}$;
(4)原式=2a-$\sqrt{3a}$a+2a$\sqrt{3a}$=2a+a$\sqrt{3a}$;
(5)原式=$\frac{(a+1+\sqrt{{a}^{2}-1})^{2}+(a+1-\sqrt{{a}^{2}-1})^{2}}{(a+1-\sqrt{{a}^{2}-1})(a+1+\sqrt{{a}^{2}-1})}$=$\frac{2(a+1)^{2}+2({a}^{2}-1)}{(a+1)^{2}-({a}^{2}-1)}$=2
点评 本题考查了二次根式的化简求值,正确掌握乘法公式是关键.


科目:初中数学 来源: 题型:解答题
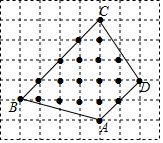 我们在计算不规则图形的面积时,有时采用“方格法”来计算.计算方法如下:假定每个小方格的边长为1个单位长度.S为图形的面积,L是边界上的格点数,N是内部格点数,则有S=$\frac{L}{2}$+N-1.请根据此方法计算图中四边形ABCD的面积.
我们在计算不规则图形的面积时,有时采用“方格法”来计算.计算方法如下:假定每个小方格的边长为1个单位长度.S为图形的面积,L是边界上的格点数,N是内部格点数,则有S=$\frac{L}{2}$+N-1.请根据此方法计算图中四边形ABCD的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
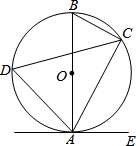 如图已知AB是⊙O的直径,AB=10,点C,D在⊙O上,DC平分∠ACB,点E在⊙O外,∠EAC=∠D.
如图已知AB是⊙O的直径,AB=10,点C,D在⊙O上,DC平分∠ACB,点E在⊙O外,∠EAC=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
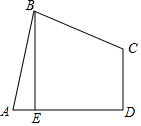 如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为16,则BE=( )
如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为16,则BE=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com