
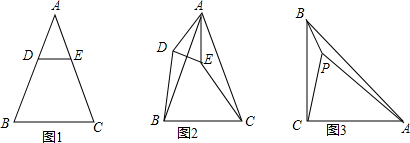
分析 (1)由DE∥BC,得到$\frac{DB}{AB}=\frac{EC}{AC}$,结合AB=AC,得到DB=EC;
(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;
(3)由旋转构造出△CPB≌△CEA,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEA是直角三角形,在简单计算即可.
解答 解:(1)∵DE∥BC,
∴$\frac{DB}{AB}=\frac{EC}{AC}$,
∵AB=AC,
∴DB=EC,
故答案为:=,
(2)成立.
证明:由①易知AD=AE,
∴由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中
得$\left\{\begin{array}{l}AD=AE\\∠DAB=∠EAC\\ AB=AC\end{array}\right.$
∴△DAB≌△EAC,
∴DB=CE,
(3)如图,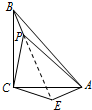
将△CPB绕点C旋转90°得△CEA,连接PE,
∴△CPB≌△CEA,
∴CE=CP=2,AE=BP=1,∠PCE=90°,
∴∠CEP=∠CPE=45°,
在Rt△PCE中,由勾股定理可得,PE=2$\sqrt{2}$,
在△PEA中,PE2=(2$\sqrt{2}$)2=8,AE2=12=1,PA2=32=9,
∵PE2+AE2=AP2,
∴△PEA是直角三角形
∴∠PEA=90°,
∴∠CEA=135°,
又∵△CPB≌△CEA
∴∠BPC=∠CEA=135°.
点评 此题是几何变换综合题,主要考查了旋转的性质,平行线的性质,全等三角形的性质和判定,勾股定理及其逆定理,解本题的关键是构造全等三角形,也是本题的难点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2)且tan∠ABC=$\frac{1}{2}$;
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2)且tan∠ABC=$\frac{1}{2}$;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(5,0),菱形OABC的顶点B,C都在第一象限,tan∠AOC=$\frac{4}{3}$,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG.
如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(5,0),菱形OABC的顶点B,C都在第一象限,tan∠AOC=$\frac{4}{3}$,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com