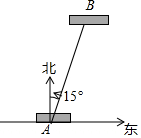
如图.一艘船在A处遇险后向相距50 海里位于B处的救生船报警．用方向和距离描述遇险船相对于救生船的位置南偏西15°.50海里．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

17．

如图，一艘船在A处遇险后向相距50 海里位于B处的救生船报警．用方向和距离描述遇险船相对于救生船的位置南偏西15°，50海里．

分析直接根据题意得出AB的长以及∠ABC的度数，进而得出答案．

解答解：由题意可得：∠ABC=15°，AB=50海里，
故遇险船相对于救生船的位置是：南偏西15°，50海里，
故答案为：南偏西15°，50海里．

点评此题主要考查了坐标确定位置，正确理解方向角的定义是解题关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

7．某企业对其生产的产品进行抽检，抽检结果如下表：

抽检件数	10	40	100	200	300	500
不合格件数	0	1	2	3	6	10

若该企业生产该产品10000件，估计不合格产品的件数为（　　）

A．

80件

B．

100件

C．

150件

D．

200件

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

8．已知$\frac{2x-1}{3}$-1≥x-$\frac{5-3x}{2}$，求|x-1|-|x+3|的最小值-3$\frac{3}{11}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．如图1，∠A₁BC、∠A₁CM的角平分线BA₂、CA₂相交于点A₂，
（1）如果∠A₁=68°，那么∠A₂的度数是多少，试说明理由；
（2）如图2，如果∠A₂BC、∠A₂CM的角平分线BA₃、CA₃相交于点A₃，请直接写出∠A₃的度数；
（3）如图2，重复上述过程，∠A_n-1BC、∠A_n-1CM的角平分线BA_n、CA_n相交于点A_n得到∠A_n，设∠A₁=θ，请用θ表示∠A_n（直接写出答案）
解：（1）结论：∠A₂=34度．说理如下：因为BA₂、CA₂平分∠A₁BC和∠A₁CM（已知），
所以∠A₁BC=2∠1，∠A₁CM=2∠2（角平分线的定义）．
因为∠A₁CM=∠A₁BC+∠∠A₁，∠2=∠1+∠A₂（三角形的一个外角等于与它不相邻的两个内角的和），
（完成以下说理过程）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

12．估算$\sqrt{21}$-2的值（　　）

A．

在1到2之间

B．

在2到3之间

C．

在3到4之间

D．

在4到5之间

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．

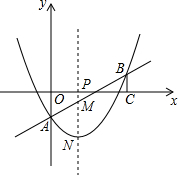如图所示，抛物线y=$\frac{1}{4}$x²+mx+n与直线y=$\frac{1}{2}$x-2相交于点A和点B，其中点A在y轴上，过点B作BC⊥x铀，垂足为点C（6，0）．
（1）求抛物线的解析式；
（2）点P是线段OC上一点．过点P作PM⊥x轴交直线AB于点M，交抛物线于点N．若设点P的坐标为（t，0），线段MN的长为s，求s与t的函数关系式；
（3）连接MB、NC，是否存在点P使四边形MNCB为平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．

直线y=$\frac{3}{2}$x与双曲线y=$\frac{k}{x}$的交点A的横坐标为2
（1）求k的值
（2）如图，过点P（m，3）（m＞0）作x轴的垂线交双曲线y=$\frac{k}{x}$（x＞0）于点M，交直线OA于点N
①连接OM，当OA=OM时，直接写出PN-PM的值
②试比较PM与PN的大小，并证明你的结论．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成图1．
探索发现：试用不同的方法计算图1的面积，你能发现a、b、c间有什么数量关系？
尝试应用：如图2，在直角三角形ABC中，∠ACB=90°，三边分别为a、b、c，
①若b-a=2，c=10，求此三角形的周长及面积．
②若b=12，a、c均为整数，试求出所有满足条件的a、c的值．